Trong học hình học, việc tính đường cao trong tam giác là một phần quan trọng, giúp chúng ta hiểu rõ mối quan hệ, tính chất của các đỉnh trong tam giác. Công thức tính độ cao trong các dạng tam giác khác nhau là điều chúng ta thường gặp và áp dụng. Hãy cùng tìm hiểu sâu hơn cách tính từng trường hợp tam giác vuông, tam giác đều, tam giác cân, tam giác đều và ứng dụng thực tế của nó trong bài viết dưới đây.
Công thức tính đường cao trong tam giác
1. Tìm độ cao trong tam giác đều
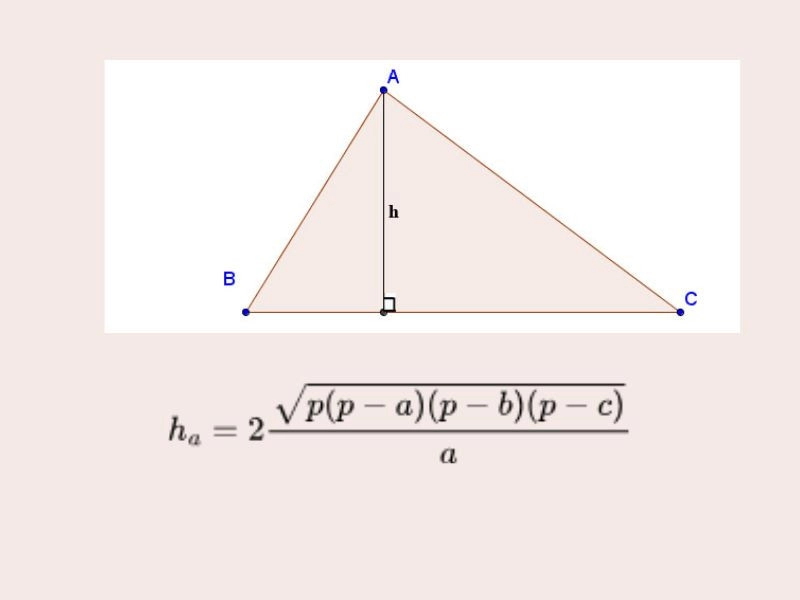
Trong đó:
- a, b, c là độ dài các cạnh;
- h là đường cao hạ từ đỉnh A xuống cạnh BC
- p là nửa chu vi: p = (a+b+c) / 2
Ví dụ:
Cho tam giác ABC có cạnh AB = 4 cm, cạnh BC = 7 cm, cạnh AC = 5 cm. Tính đường cao AH từ A cắt BC tại H và tính diện tích ABC.
Phần thưởng:
Nửa chu vi tam giác: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8(cm)
Chiều cao của hình tam giác
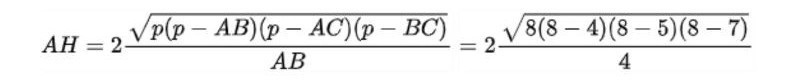
=> AH = 4√8
Xét tam giác ABC, ta có:

Đáp án: AH = 4√8, S = 14√8
2. Công thức tính độ cao trong tam giác cân
 Tam giác ABC cân tại H
Tam giác ABC cân tại H
Giả sử bạn có tam giác ABC cân tại A, đường cao AH vuông góc tại H như hình trên:
Công thức tính lượng đường cao AH:
Vì tam giác ABC cân tại A nên đường cao AH cũng là đường trung tuyến nên:
⇒ HB=HC= ½BC
Áp dụng định lý Pythagore cho tam giác vuông ABH ngay tại H ta có:
AH2 + BH2 = AB2
⇒ AH2 = AB2 − BH2
Ví dụ: Cho Δ ABC cân bằng tại A có BC = 30(cm), độ cao AH = 20(cm). Tính độ cao tương ứng với cạnh của tam giác cân đó.
Lời giải: Xét Δ ABC cân tại A với BC = 30(cm)
⇒ BH = CH = 15(cm).
Áp dụng định lý Py-ta-go ta có:

3. Tính độ cao trong tam giác đều
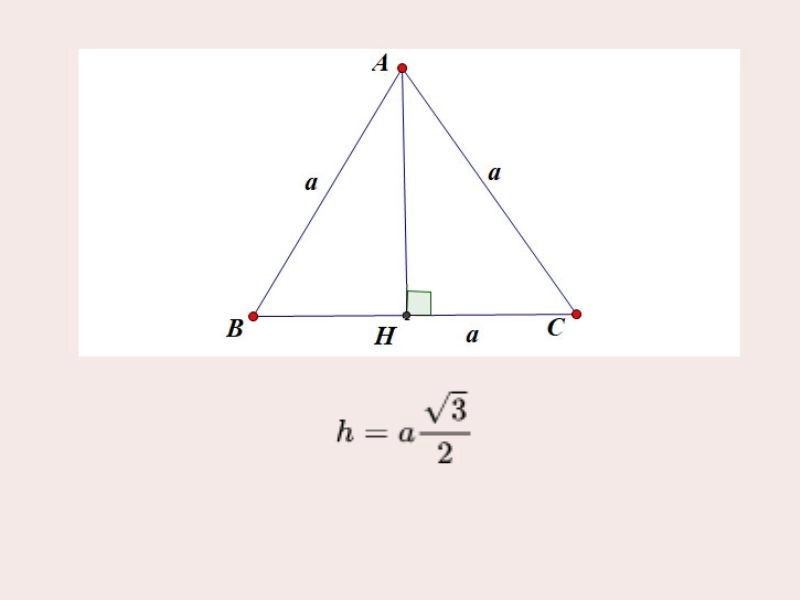
Trong đó:
- h là đường cao của tam giác đều
- a là độ dài cạnh của tam giác đều
Ví dụ:
Cho tam giác đều ABC, cạnh AB = BC = AC = a = 6, vẽ đường cao từ A xuống cắt BC tại H, tính đường cao AH.
Phần thưởng:
Xét tam giác đều ABC, dựa vào công thức tính đường cao ta có:
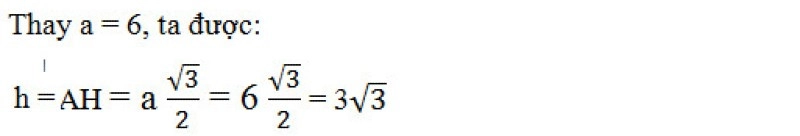
3. Công thức tính độ cao trong tam giác vuông
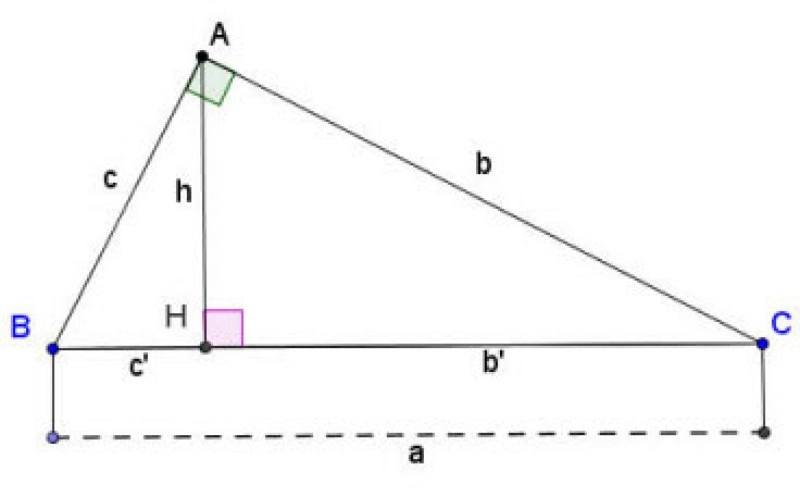 Tam giác vuông ABC
Tam giác vuông ABC
Công thức tính cạnh và đường cao trong tam giác vuông:
1. a2 = b2 + c2
2. b2 = ab′ và c2 = ac′
3. à = bc
4. h2 = b′.c'
5. 
Trong đó:
- a, b, c là các cạnh của tam giác vuông như hình trên;
- b' là hình chiếu của cạnh b lên cạnh huyền;
- c' là hình chiếu của cạnh c lên cạnh huyền;
- h là chiều cao của tam giác vuông vẽ từ đỉnh góc vuông A đến cạnh huyền BC
Ví dụ: Cho tam giác vuông ABC tại A, AB=24cm, AC=32cm. Đường trung trực của BC cắt AC và BC theo thứ tự D và E. Tính DE.
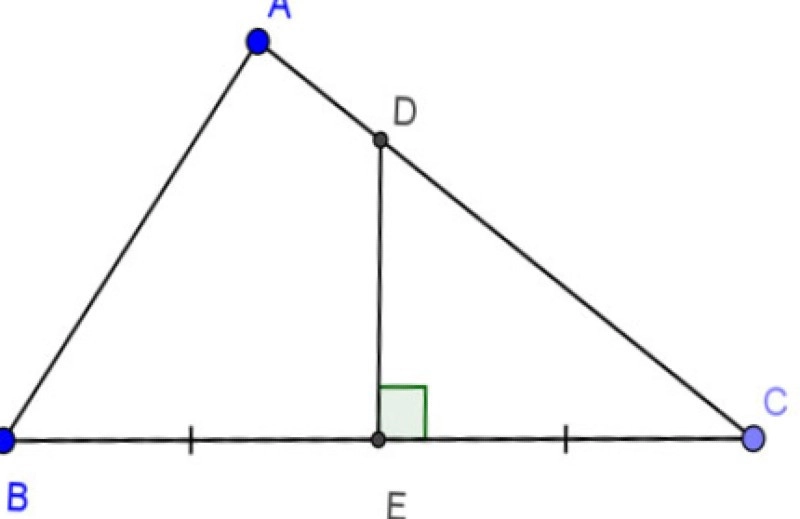 Tam giác vuông ABC
Tam giác vuông ABC
Phần thưởng:
Xét tam giác vuông ABC, ta có:
BC2 = AB2+ AC2 (theo định lý Pythagore)
BC2 = 242+ 322
BC2 = 1600
BC = 40(cm)
EC = BC : 2 = 40 : 2 = 20(cm)
Xét tam giác vuông ACB và tam giác vuông ECD, ta có:
Có ∠A = ∠E = 90o
∠C chung
=> Tam giác ACB ∾ tam giác ECD (gg)
=> AC/EC = AB/ED
=> ED = AB.EC/AC = 15cm
Vậy ED = 15cm
Xác định đường cao trong tam giác
Đường cao trong một tam giác là đoạn thẳng nối một đỉnh của tam giác với đường thẳng chứa cạnh đối diện của đỉnh đó và vuông góc với cạnh đó. Độ cao có thể ở trong tam giác, ngoài tam giác hoặc trùng với một cạnh của tam giác.
Độ cao có thể dùng để tính diện tích hình tam giác theo công thức: S = 1/2 xaxh, trong đó a là độ dài cạnh đáy và h là chiều cao của đường cao tương ứng.
Tính chất ba đường cao của một tam giác
Ba đường cao của tam giác đều đi qua một điểm. Điểm đó gọi là trực tâm của tam giác.
Các công thức trên cho phép chúng ta xác định chiều cao của một tam giác một cách chính xác nhất khi biết độ dài cạnh huyền và cạnh góc vuông kề với đường cao. Từ này có thể được sử dụng để tìm góc vuông kề với đường cao khi biết độ dài cạnh huyền và đường cao. Hy vọng bài viết trên Fresh Lemon Review đã giúp các bạn hiểu rõ công thức tính độ cao trong hình tam giác và áp dụng dễ dàng nhất.























Ý kiến bạn đọc (0)