Công thức tính diện tích hình bình hành chính xác nhất 2023 và bài tập

Công thức để xác định diện tích hình bình hành là gì? Trong bài viết dưới đây Thác Trầm Hương Mobile sẽ cung cấp cho các bạn một số công thức, thông tin để có thể tính diện tích hình bình hành một cách chính xác. Bên cạnh đó bài viết sẽ cung cấp cho các bạn một số bài tập có đáp án đầy đủ để các bạn có thể luyện tập.

Tìm hiểu về hình bình hành

Trước khi tìm hiểu về diện tích hình bình hành, bạn cần hiểu rõ khái niệm, đặc điểm của loại hình học này. Hình bình hành là một tứ giác thuộc hình học không gian phẳng 2 chiều. Hình bình hành là một tứ giác được tạo thành từ hai cặp cạnh đối song song, đối diện và bằng nhau. Đặc biệt, các góc đối diện có số đo bằng nhau. Điểm nổi bật của hình bình hành là tứ giác, hai cặp cạnh đối song song, đối diện và bằng nhau.

Hiện nay, hình bình hành được sử dụng rộng rãi trong nhiều ngành nghề. Bao gồm kiến ​​trúc, thiết kế, xây dựng và kỹ thuật, công nghệ và khoa học. Hình bình hành được định nghĩa là một trong những khái niệm hình học cơ bản trong hình học trong toán học.

Hình bình hành có thể là hình chữ nhật có 4 cạnh vuông góc hoặc hình thoi có các cạnh bằng nhau và các góc đối diện có cùng độ lớn. Đặc biệt, khái niệm hình bình hành đều là hình có 4 cạnh bằng nhau, các góc đối diện bằng nhau và độ lớn bằng nhau.

Khái niệm diện tích hình học là gì?

Trước khi tìm hiểu về thuật ngữ diện tích hình bình hành, chúng ta cần hiểu rõ thuật ngữ diện tích hình học. Vì vậy, diện tích hình học là toàn bộ diện tích tính toán của phần mặt phẳng bên trong hình đó, nghĩa là lượng không gian được bao phủ và biểu thị tổng số đơn vị không gian chiếm bên trong hình đó.

Những ngành nghề này bao gồm xây dựng, kiến ​​trúc, thống kê, khoa học và tự nhiên. Ngoài ra, diện tích còn là một khái niệm cơ bản, là bước đệm cho các khái niệm khác trong lĩnh vực hình học nói riêng và toán học nói chung.

Vì vậy, việc nắm bắt, hiểu và thực hành các khái niệm về diện tích hình học là vô cùng quan trọng trong lĩnh vực toán học và các ngành nghề liên quan. Thuật ngữ diện tích sẽ giúp xác định, tính toán và đo lường các hình dạng và kích thước khác. Đồng thời, thuật ngữ diện tích hình học sẽ là nền tảng để xây dựng các khái niệm toán học khác. Vì vậy, nếu là người đam mê toán học, bạn có thể nghiên cứu để áp dụng chính xác các thuật ngữ khu vực vào thực tế.

Khái niệm diện tích hình bình hành là gì?

Dựa vào khái niệm diện tích hình học đã phân tích ở trên, có thể rút ra kết luận về khái niệm diện tích hình bình hành. Như vậy, diện tích của hình bình hành là tổng đơn vị của phần mặt phẳng nhìn ra bên ngoài so với hình không gian. Thông thường, để có thể tính diện tích hình bình hành, bạn cần có công thức chính xác nhất. Điều này sẽ giúp tránh được những sai sót khi sử dụng và tính toán. Để tính diện tích hình bình hành, chúng ta cần xác định chiều dài và chiều rộng của hình đó.

Tiếp theo chúng ta sẽ áp dụng công thức tính diện tích hình bình hành kết hợp với số đo để có được kết quả. Đặc biệt, diện tích hình bình hành còn được tính bằng công thức sử dụng chiều dài đường chéo và chiều cao của hình.

Lưu ý, khi tính diện tích hình bình hành, các bạn cần chú ý đến đơn vị đo cần sử dụng. Diện tích khi đo sẽ bằng đơn vị chiều dài bình phương như mét vuông hay cm vuông. Khi lựa chọn sử dụng đơn vị khác, bạn cần phải thống nhất với đơn vị đó để đảm bảo tính chính xác và thống nhất của kết quả.

Công thức xác định diện tích hình bình hành

Diện tích của hình bình hành được xác định bởi kích thước bề mặt của hình đó, tức là kích thước của mặt phẳng mà chúng ta có thể nhìn thấy bên ngoài.

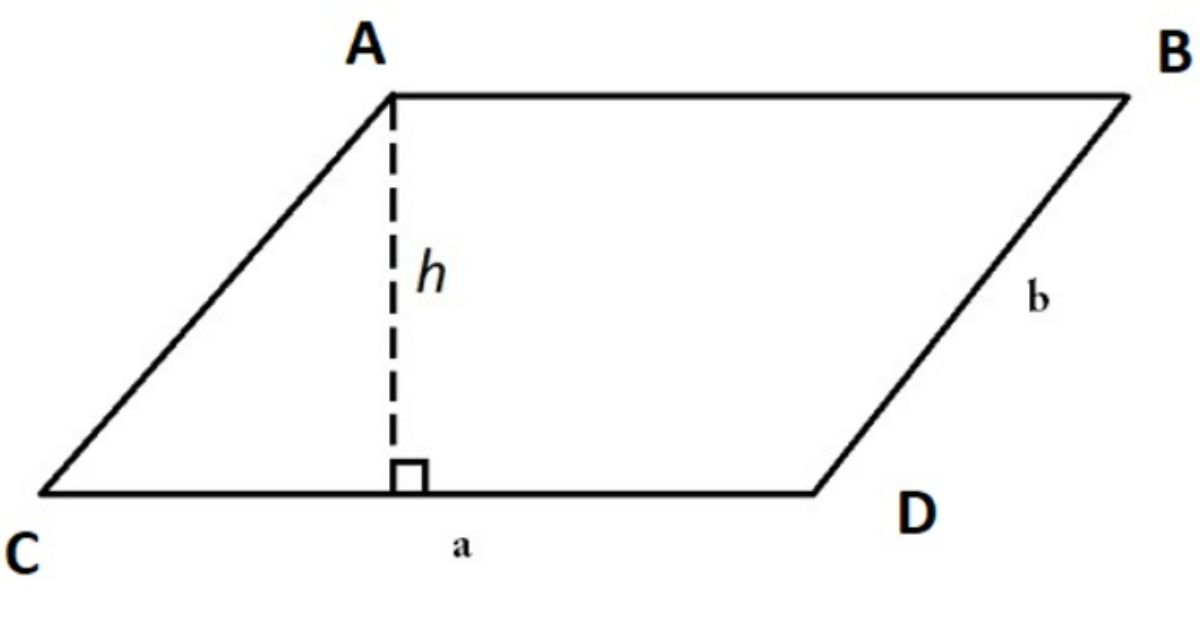
Công thức xác định diện tích hình bình hành được tính bằng cách nhân chiều cao với cạnh đáy. Với công thức: S=ax h.

Các yếu tố trong công thức tính diện tích hình bình hành bao gồm:

• S là diện tích tính toán của hình bình hành.
• a là số đo đáy của hình bình hành.
• h là số đo chiều cao, tính từ trên xuống dưới của hình bình hành.

Chiều cao của hình bình hành là khoảng cách từ một cạnh của hình đến một đường thẳng song song với cạnh đó và đi qua đỉnh của hình. Cạnh đáy của hình bình hành là một trong hai cạnh song song với chiều cao của hình đó. Khi nhân đáy với chiều cao, chúng ta đang tính tổng diện tích của các hình chữ nhật nhỏ được tạo bởi các cạnh của hình bình hành và chiều cao.

Như vậy, công thức tính cạnh đáy nhân với chiều cao để tính diện tích hình bình hành là cách tính diện tích hình bình hành này hợp lý và chính xác. Ngoài ra, công thức này cũng rất dễ áp ​​dụng trong thực tế.

Ví dụ áp dụng công thức: Một hình bình hành có đáy là 7 cm và chiều cao là 9 cm. Diện tích hình bình hành được xác định theo công thức sau:

Diện tích được tính là: S= axh= 7 cm x 9 cm= 63 cm2.

Làm thế nào để tính diện tích hình bình hành mà không cần đo chiều cao?

Để tính diện tích hình bình hành không cần đo chiều cao, chúng ta có thể sử dụng một trong các phương pháp sau:

Sử dụng công thức tính diện tích hình bình hành dựa vào đường chéo và một cạnh

Diện tích của hình bình hành bằng ½ tích của đường chéo và cạnh bất kỳ. Công thức: S= ½ xdxa

Trong đó:

• S được hiểu là diện tích hình bình hành (đơn vị diện tích)
• d được hiểu là độ dài đường chéo của hình bình hành (đơn vị đo chiều dài).
• a được hiểu là độ dài cạnh bất kỳ của hình bình hành (đơn vị đo độ dài).

Sử dụng công thức tính diện tích hình bình hành dựa vào hai cạnh và một góc

Diện tích hình bình hành bằng ½ tích hai cạnh và sin góc giữa hai cạnh.

Công thức: S= ½ xaxbx sin (α)

Trong đó:

• S được định nghĩa là diện tích hình bình hành (đơn vị diện tích)
• a được định nghĩa là độ dài một cạnh của hình bình hành (đơn vị đo chiều dài).
• b được định nghĩa là độ dài cạnh kề với cạnh a (đơn vị đo chiều dài).
• α được định nghĩa là góc giữa hai cạnh a và b (đơn vị đo góc)

Áp dụng tính chất của hình bình hành

Diện tích của hình bình hành bằng diện tích của hình chữ nhật có cùng chiều dài đáy và chiều cao với hình bình hành. Hoặc, diện tích hình bình hành bằng diện tích hình thoi có cùng chiều dài cạnh và chiều cao với hình bình hành.

Để sử dụng phương pháp này, chúng ta cần biết số đo chính xác độ dài một cạnh và chiều cao của hình bình hành đó. Sau đó, sử dụng công thức tính diện tích hình chữ nhật hoặc hình thoi để tính diện tích.

Ứng dụng diện tích hình bình hành trong các lĩnh vực khác

Ngoài việc được sử dụng rộng rãi trong toán học, diện tích hình bình hành còn được ứng dụng trong các lĩnh vực khác như:

• Trong lĩnh vực xây dựng, diện tích hình bình hành được dùng để xác định diện tích sàn, mặt bằng tầng của một ngôi nhà, căn hộ hay sân vườn. Tính diện tích giúp xác định vật liệu xây dựng, vật liệu lát sàn, gạch ốp lát,…
• Trong lĩnh vực thiết kế nội thất, diện tích hình bình hành sẽ được dùng để xác định diện tích không gian sao cho có thể bố trí được đồ nội thất thật. Tính toán diện tích sẽ giúp tối ưu hóa không gian và đảm bảo vật liệu được sắp xếp hợp lý.
• Trong lĩnh vực công nghệ, diện tích hình bình hành sẽ được sử dụng để hỗ trợ cho việc thiết kế các bảng mạch hoặc bố trí các linh kiện khác. Điều này sẽ giúp việc xác định không gian cho các bộ phận và loại mạch khác nhau trên bề mặt sản phẩm trở nên dễ dàng hơn.
• Trong lĩnh vực giáo dục và nghiên cứu, diện tích hình bình hành là một khái niệm hình học cơ bản được áp dụng trong toán tiểu học và trung học cơ sở.

Một số dạng bài tập tính diện tích hình bình hành

Sau khi hiểu được công thức tính diện tích hình bình hành và ứng dụng của nó trong các lĩnh vực khác nhau, bạn cần biết thêm một số bài tập cơ bản.

• Dạng 1: Tính diện tích hình bình hành khi biết độ dài cạnh đáy và số đo chiều cao. Cách làm: sử dụng công thức S= axh để tính diện tích hình bình hành.
• Dạng 2: Tính độ dài cạnh đáy khi có diện tích hình và chiều cao. Cách làm: Sử dụng công thức S= axh rồi suy ra công thức tính độ dài cạnh đáy là a = S:h.
• Dạng 3: Tính chiều cao khi đo diện tích và chiều dài cạnh đáy. Cách làm: Sử dụng công thức S= axh rồi suy ra công thức tính chiều dài, chiều cao h= S:a.
• Loại 4: Mẫu bài tập tổng quát, đây là dạng bài tập yêu cầu kỹ năng vận dụng kiến ​​thức đã học vào thực tế. Khi giải dạng bài tập này, bạn cần đọc kỹ nội dung bài toán, xác định loại phép toán có trong bài toán rồi đưa ra cách giải chính xác nhất.

Bài tập diện tích hình bình hành có đáp án chi tiết

Dưới đây là một số bài tập về cách tính diện tích hình bình hành có đáp án chi tiết mà các bạn có thể tham khảo:

Bài học 1: Tính diện tích hình bình hành có chiều dài đáy là 7 cm và chiều cao là 5 cm.

Phần thưởng:

Áp dụng công thức chuẩn đó S = axh => S = 7cm x 5cm = 35cm2.

Do đó, diện tích đo được của hình bình hành được tính là 35 cm².

Bài học 2: Tính diện tích hình bình hành có chiều dài đáy là 7 cm và chiều cao là 11 cm.

Phần thưởng:

Áp dụng công thức chuẩn đó S = axh => S = 7cm x 11cm = 77cm2

Do đó, diện tích đo được của hình bình hành được tính là 77 cm².

Bài học 3: Tính diện tích hình bình hành có chiều dài đáy là 6 cm và chiều cao là 5 cm.

Phần thưởng:

Áp dụng công thức chuẩn đó S = axh => S = 6cm x 5cm = 30cm2

Do đó, diện tích đo được của hình bình hành được tính là 30 cm².

Bản tóm tắt

Qua bài viết trên các bạn có thể nắm được công thức tính diện tích hình bình hành một cách chính xác và chi tiết nhất. Đồng thời các bạn còn tìm hiểu thêm về ứng dụng của công thức tính diện tích hình bình hành trong toán học và các lĩnh vực khác.

Xem thêm:

• Tính chất của trọng tâm và cách xác định trọng tâm của tam giác trong Hình học
• Chu vi của một vòng tròn là gì? Các công thức và bài tập đầy đủ nhất