Công thức tính diện tích tam giác vuông, thường, cân, đều chi tiết 2024

You are learning the formula to calculate the area of ​​a triangle, including regular triangles and special shapes such as isosceles triangles, right triangles and equilateral triangles. In today's article, Chanh Tuoi Review will answer that for you. . This is an important mathematical formula in solving exercises as well as practical applications later in life. Don't miss it!

Introduction to triangles

A triangle is a basic geometry in mathematics and geometry, characterized by three sides and three vertices. Triangles have many classifications such as equilateral, isosceles, right, acute and obtuse. You can base on the characteristics of the sides and angles of that triangle to classify.

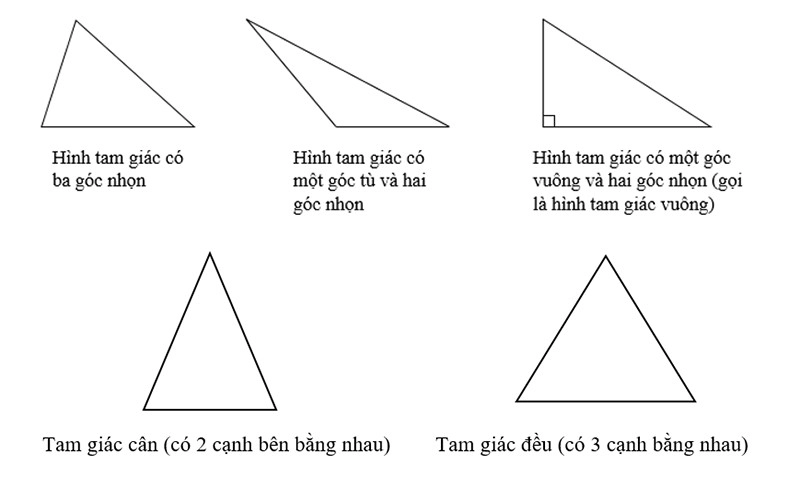Triangles come in many types with characteristic characteristics

Regarding properties, the basic properties of a triangle include the following highlights:

• The sum of three angles in a triangle is always equal to 180 degrees, called the Angle Sum Theorem in a triangle.
• Each exterior angle of a triangle is equal to the sum of the two interior angles of the triangle that do not contain it.
• In a triangle, the sum of the lengths of any two sides is always greater than the length of the remaining side.
• For a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the two sides.
• A line segment from a vertex of a triangle to a point on the opposite side divides the side into two segments with a ratio equal to the ratio of the lengths of the two remaining sides.
• The three line segments connecting the vertices of the triangle to the midpoints of the opposite side are three line segments of equal length and intersect at one point (center of gravity).
• The perimeter of a triangle is equal to the sum of the lengths of the three sides. Area can be calculated using a variety of methods such as the Heron Area Formula or using corresponding heights and sides.

VIEW DELIVIETNAM SHOP SPECIALIZED IN REPUTABLE STUDY TOOLS HERE

Summary of formulas for calculating the area of ​​a triangle are often the most accurate

A regular triangle is a triangle with different side lengths and different angle measures. To calculate the area of ​​a triangle, we can take advantage of the triangle's categorical characteristics and apply many different area formulas.

Depending on the properties of the triangle, we can use Heron's area formula if we know the three side lengths, or take advantage of the corresponding height and side of the triangle if they are known.

Right now, Chanh Tuoi Review will share with you the easiest and most accurate formula for calculating the area of ​​a regular triangle. Watch now!

Overview example images for all formulas:

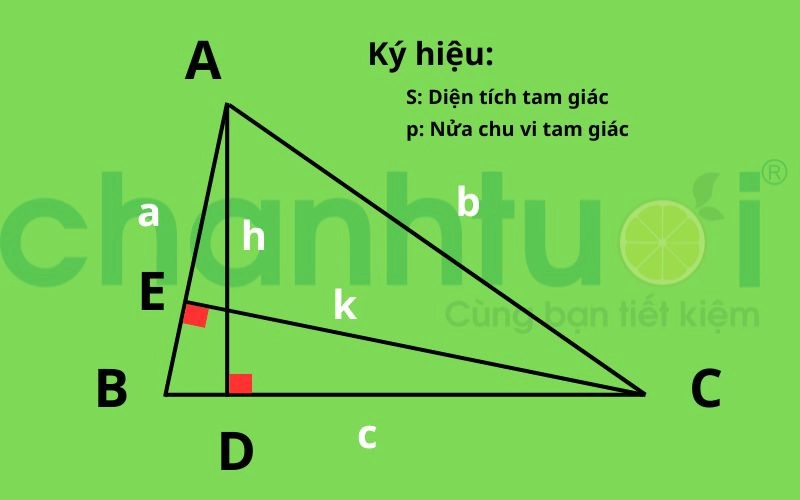Refer to this image for the formulas below

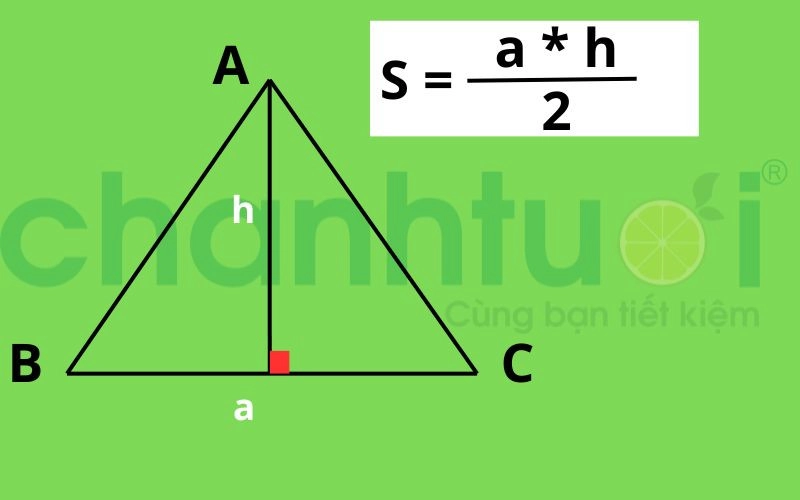
What is the formula to calculate the area of ​​a triangle?

Let S be the area of ​​the triangle. We have: Area is equal to the length of any side multiplied by the corresponding height of that side and divided by 2.

Formula: S = (a * h) : 2 = ½ (a * h)

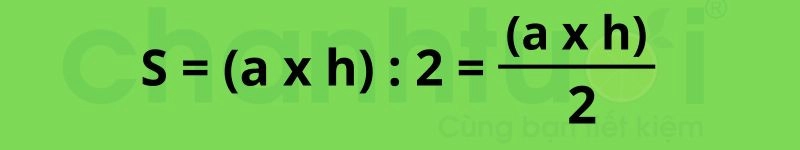How to calculate the area of ​​a regular triangle

In there:

• S is the area of ​​triangle ABC
• a is the length of side AB
• h is the corresponding height of side AB (here it is side AD)

Additionally, you can also calculate the area knowing the remaining sides. For example:

• If we take the length of side AC as b, the corresponding height side of AC is CE (denoted as k).
• The formula to calculate the area of ​​a triangle will be: S = (bxk): 2 = ½ (bxk)

Similarly, you can also perform the formula with the remaining edge.

Example: Calculate the area of ​​triangle ABC with a=5cm, h=8cm?

Applying the formula we have: S (ABC) = (5 * 8): 2 = 20cm².

Heron's area formula calculates the area of ​​a regular triangle

This Heron formula is named after the mathematician Heron of Alexandria. How to calculate the area of ​​a triangle when knowing the lengths of the three sides of the triangle.

According to the example image above, we have a, b, c being the lengths of the three sides AB, BC, AC of triangle ABC.

First, we need to calculate the half-perimeter of that triangle (p) according to the formula: p = (a + b + c)/2

At this point, Heron's formula calculates the area of ​​a regular triangle as follows: S(ABC) = √(p * (p – a) * (p – b) * (p – c))

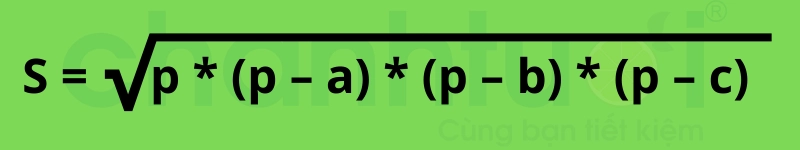Heron's formula calculates the area of ​​a regular triangle

Example: Calculate the area of ​​triangle ABC with a=5cm, b=8cm, c=5cm?

Calculate the half perimeter of the triangle p= (a + b + c)/2 = (5 + 8 + 5): 2 = 9cm

Applying the formula we have: S(ABC) = √(p * (p – a) * (p – b) * (p – c)) = √(9 * (9 – 5) * (9 – 8) * (9 – 5)) = 12cm².

BUY CASIO FX-580VN STUDY COMPUTER HERE

Use the Sine theorem to calculate the area of ​​a triangle

How to calculate the area of ​​a triangle if you know an angle and the length of 2 sides of the triangle. At this point, you can apply the Sine theorem to calculate the area.

At this point, the formula for calculating area is ½ the product of the lengths of the two sides multiplied by the sine of the angle between the two sides.

Specifically: S = ½ * a * b * sin(A) = ½ * a * c * sin(B) = ½ * b * c * sin(C)

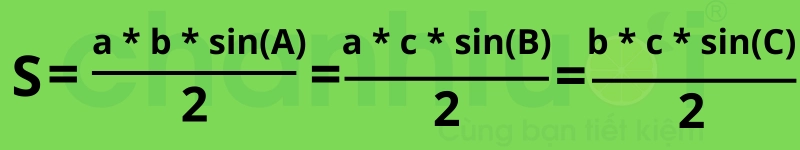Calculate the area of ​​a regular triangle using the Sine theorem

Example: Calculate the area of ​​triangle ABC with a=5cm, b=8cm and angle A equal to 48°?

Applying the formula we have: S (ABC) = ½ * a * b * sin(A) = ½ * 5 * 8 * sin(48°) = 14.86cm².

Formula to calculate the area of ​​a right triangle

A right triangle is characterized by having a right angle, where two sides meet to form a 90-degree angle. This means that the intersection of these two sides forms a right angle, which is a characteristic angle whose magnitude is exactly 90 degrees.

The formula for calculating the area of ​​a right triangle is as follows: Area is equal to the lengths of the two sides of the right angle multiplied together and divided by 2.

S = ½ (a * b) = (a * b) : 2

In which: a, b are the lengths of the two sides of the right angle

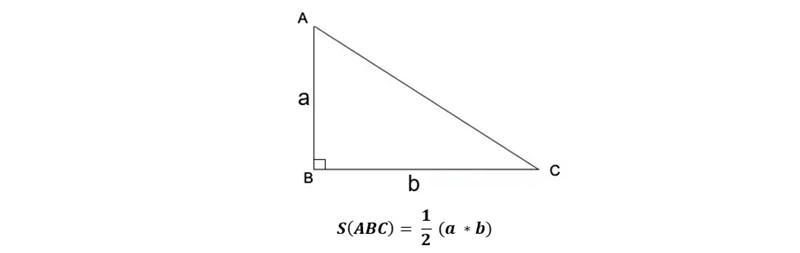Formula to calculate the area of ​​a right triangle

For example: Calculate the area of ​​a right triangle ABC with the lengths of the two sides being 5 cm and 8 cm respectively.

The area of ​​triangle ABC is now calculated as follows: ½ (5 * 8) = 20 cm².

Formula to calculate the area of ​​an isosceles triangle

An isosceles triangle is a special type of triangle, with two sides of equal length and two angles opposite these sides that are also equal in length.

The formula for calculating the area of ​​an isosceles triangle is calculated as follows: Area is equal to the length of the remaining side multiplied by the corresponding height of that side and then divided by 2.

How to calculate the area of ​​an isosceles triangle

Specifically: S = ½ (a * h) = (a * h) : 2

In there:

• a is the length of the remaining side other than the two sides of equal length (BC)
• h is the height connecting the top of the opposite corner of that side to the bottom

For example: Let the isosceles triangle ABC have sides AB and AC of equal length, side BC has a length of 10 cm. The length connecting vertex A to BC is 6 cm. The area of ​​isosceles triangle ABC is calculated as follows: S(ABC) = ½ (10 * 6) = 30 cm².

Formula to calculate the area of ​​an isosceles right triangle

An isosceles right triangle is a special type of right triangle, with two sides of equal length, forming a right angle, and at the same time two sides of right angles. The formula for calculating the area of ​​an isosceles right triangle is calculated as follows: Area is equal to the length of one side of a right angle squared then divided by 2.

Specifically: S = ½ * (a²) = a²/2

In which: a is the length of two equal sides of right angles AB and AC.

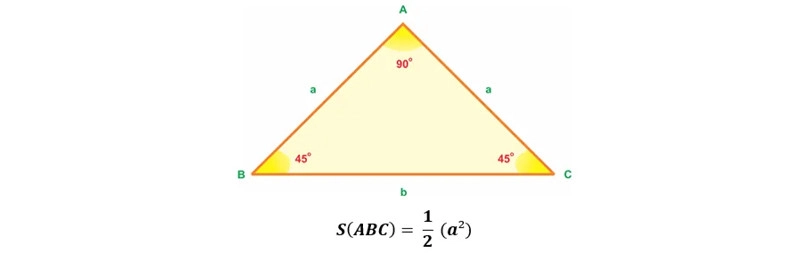How to calculate the area of ​​an isosceles right triangle

Example: Calculate the area of ​​an isosceles right triangle ABC with the length of two sides of the right angle being 6 cm.

The area of ​​triangle ABC is calculated as follows: S(ABC) = ½ (6²) = 13 cm².

Formula to calculate the area of ​​an equilateral triangle

An equilateral triangle is a special type of triangle, with three equal sides and three equal angles. That is, all sides of the triangle are equal in length and all angles of the triangle are exactly 60 degrees.

The formula for calculating the area of ​​an equilateral triangle with side a is calculated as follows: Area is equal to the length of any side multiplied by any height and divided by 2.

Specifically: S = (a * h) : 2 = 1/ 2 * (a * h)

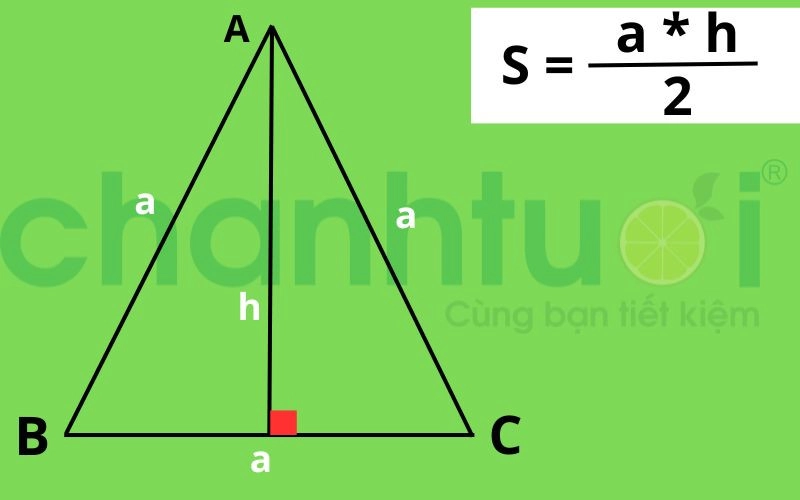How to calculate the area of ​​an equilateral triangle

In there:

• a is the length of any side (in an equilateral triangle, the lengths of all 3 sides are equal)
• h is any height (in an equilateral triangle, the heights of all sides are equal)

For example: Calculate the area of ​​an equilateral triangle ABC with equal sides and 6cm, the height from vertex A to side BC is 4cm.

The area of ​​triangle ABC is calculated as follows: S(ABC) = ½ (6 * 4) = 12 cm².

BUY A SET OF RULES, DEGREE MEASUREMENTS, STUDENT EKE HERE

Formula to calculate the area of ​​a triangle in Oxyz

In the Oxyz coordinate system, a triangle is a three-sided polygon located in three-dimensional space and determined by three points located on the same line. These points are represented through coordinates (x, y, z), with x, y and z being real numbers representing the point's position in space.

The area of ​​triangle ABC in the Oxyz coordinate system is calculated as half the absolute value of the third product of two vectors AB and AC. In this formula, AB and AC are two vectors represented on the Oxyz axis.

Specifically:

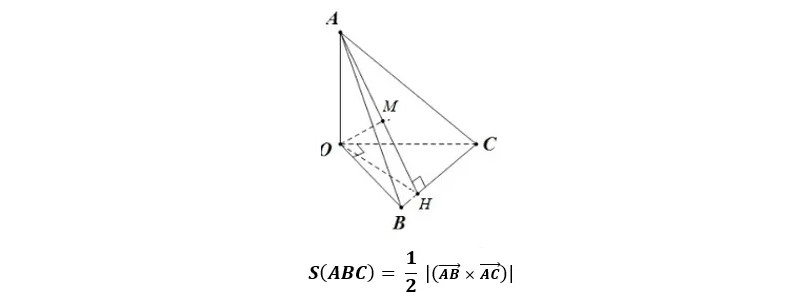How to calculate the area of ​​a triangle in Oxyz

For example: On the coordinate system for triangle ABC there are 3 points A(-1; 1; 2), B(1; 2; 3), C(3; – 2; 0). The area of ​​triangle ABC is calculated as follows:

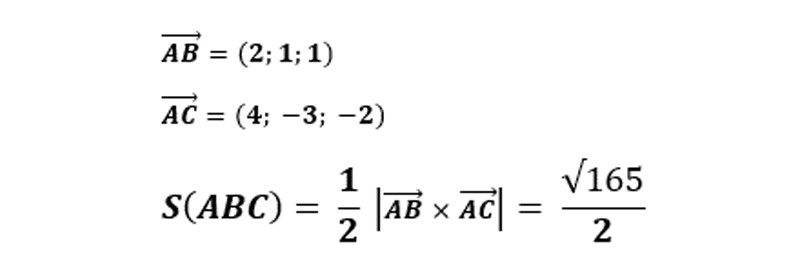Solve the problem to calculate the area of ​​triangle ABC

Some exercises to calculate the area of ​​typical triangles with detailed solutions

Based on the presented knowledge and formulas, you have gained a solid understanding of how to calculate the area of ​​a triangle when applying them to specific exercises. If you still have difficulty figuring out how to solve exercises effectively, below are some practice exercises from basic to advanced that you can refer to to improve your skills.

Exercise 1

Triangle ABC is a right triangle at A, with height h = 6 cm. The length of the side of the square is 8 cm. Calculate the area of ​​triangle ABC.

Solution:

Because triangle ABC is a right triangle at A, we know that the side of the right angle has length 8 cm and height h = 6 cm.

Calculate the area of ​​a triangle (S) using the triangle area formula: S = (1/2) * sides * height.

S = (1/2) * 8 cm * 6 cm = 24 cm². So the area of ​​triangle ABC is 24 cm².

Exercise 2

Right triangle ABC has side AB with length 10 cm and area S = 40 cm². Calculate the length of hypotenuse BC of right triangle ABC.

Solution:

We know that right triangle ABC has side AB with length 10 cm and area S = 40 cm².

Step 1: Calculate the length of the remaining square side AC = (S * 2)/ AB = (40 * 2)/10 = 8 cm

Step 2: Calculate the length of hypotenuse BC of a right triangle. Based on the Pythagorean formula, the square of the hypotenuse is equal to the sum of the squares of the two sides of the right angle.

Therefore (BC)².= (AB)². + (AC)². = 10². + 8². = 164 → BC = √164 = approximately 12.9 cm.

Exercise 3

Triangle ABC has three side lengths: AB = 6 cm, BC = 8 cm and AC = 10 cm. Calculate the area of ​​triangle ABC.

Solution:

To calculate the area of ​​a triangle when we know the lengths of the three sides, we use Heron's formula. This formula is used to calculate the area of ​​a triangle when the lengths of the three sides are known.

Heron's formula: Area of ​​triangle ABC (S) = √(p * (p – a) * (p – b) * (p – c))

Step 1: Calculate half the perimeter p of the triangle: p = (6 cm + 8 cm + 10 cm) / 2 = 24 cm / 2 = 12 cm

Step 2: Calculate the area of ​​the triangle (S) using Heron's formula.

• S = √(12 cm * (12 cm – 6 cm) * (12 cm – 8 cm) * (12 cm – 10 cm))
• S = √(12 cm * 6 cm * 4 cm * 2 cm) = √(576 cm²) = 24 cm²

So the area of ​​triangle ABC is 24 cm².

You may also be interested in how to calculate the area of ​​a trapezoid:

• The most accurate formula for calculating the area of ​​a trapezoid

Above are detailed instructions for the most accurate formula for calculating the area of ​​a triangle. Please write it down so it's easier to remember!