Công thức tính thể tích hình cầu và diện tích hình cầu

Công thức tính thể tích, diện tích hình cầu là những kiến ​​thức mà học sinh cần nắm vững để chuẩn bị cho kỳ thi sắp tới. Việc nắm rõ công thức này còn giúp các bạn ôn thi và làm bài nhanh hơn. Nếu bạn vẫn chưa hiểu rõ về hình cầu và các công thức xung quanh nó thì có thể tìm hiểu qua bài viết sau.

Hình cầu hoặc hình cầu là gì?

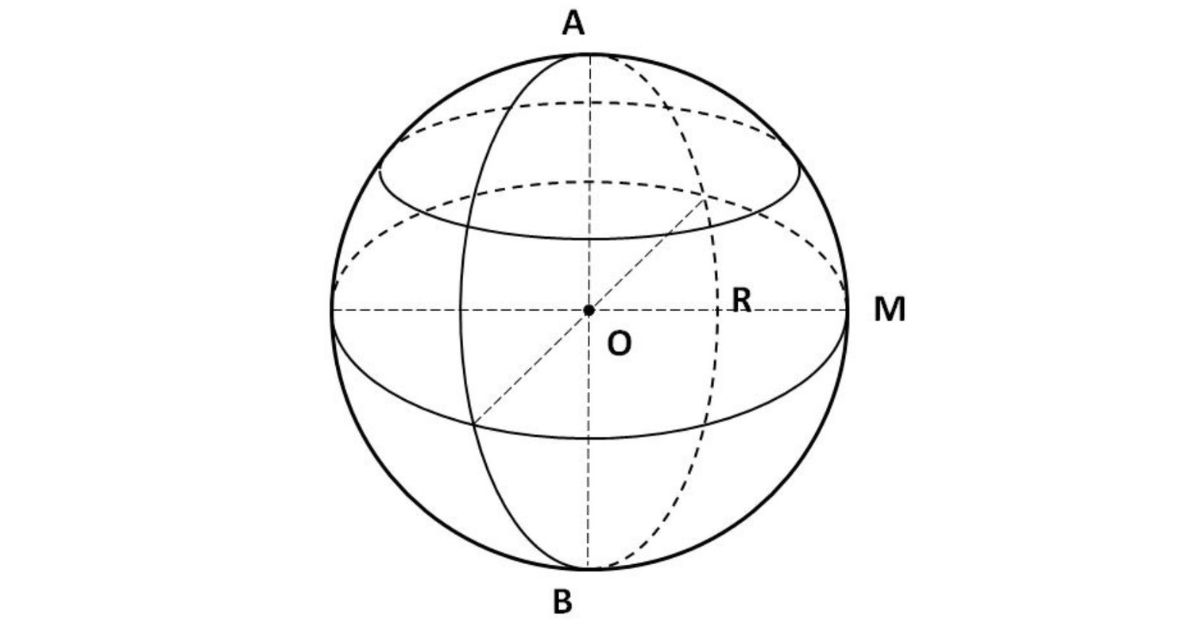
Trước khi tìm hiểu về thể tích và diện tích hình cầu, chúng ta phải tìm hiểu về hình cầu và hình cầu. Trong không gian 3 chiều, theo toán học, khi quay nửa hình tròn (bán kính tâm O và R) quanh một đường kính cố định gọi là AB, ta sẽ có một hình cầu:

• Nửa đường tròn của phép quay trên là hình cầu.
• O được coi là tâm của hình cầu và R là bán kính bên trong hình cầu hoặc hình cầu đó.

Một hình cầu là gì?

Hình cầu bao gồm các điểm nằm cách tâm O của hình cầu một khoảng cố định và không đổi. Đây là bán kính R và R = OA.

Mặt cầu là gì?

Ngoài ra, hình cầu còn có một số tính chất như sau:

• Bất kỳ đường thẳng nào cắt hình cầu và sau đó đi qua tâm của hình cầu đều là trục đối xứng trong hình cầu. Khi đó, việc quay một quả cầu quanh trục đối xứng, bất kể góc nào, cũng khiến nó trở thành chính nó.
• Mặt phẳng phản xạ của hình cầu là mặt phẳng có thể cắt hình cầu đi qua tâm của hình cầu và chia hình đó thành hai phần bằng nhau.

Công thức tính thể tích hình cầu và diện tích hình cầu

Sau khi tìm hiểu sơ qua về hình cầu và bề mặt cầu, tiếp theo hãy tìm hiểu công thức tính diện tích và thể tích hình cầu như sau:

Công thức tính diện tích (S) hình cầu

Theo quan niệm trên thì hình cầu S có giá trị gấp 4 lần S của một hình tròn lớn hoặc gấp 4 lần số Pi(π) nhân với bán kính bình phương của hình cầu.

Như vậy, cách tính diện tích hình cầu là: S = 4π xr^2 = π xd^2

Trong đó:

• S: Diện tích hình cầu
• r: Bán kính hình cầu/mặt cầu
• d: Đường kính hình cầu/bề mặt hình cầu
• π: hằng số xấp xỉ 3,14

Công thức tính diện tích (S) hình cầu

Công thức tính diện tích (S) hình cầu

Để tính S hình cầu, bạn sử dụng công thức: Sxq = 4 x π xr^2

Trong đó:

• Sxq: Diện tích hình cầu
• π: Hằng số 3,14
• r: bán kính hình cầu

Công thức tính diện tích (S) hình cầu

Công thức tính thể tích (V) của hình cầu

Để tính thể tích của hình cầu, bạn cần tìm bán kính của hình cầu hoặc tìm đường kính của hình cầu. Tiếp theo, bạn thay thế chúng cho công thức sau:

V = (4 x π xr^3)/ 3

Trong đó:

• V: Thể tích của quả cầu (m3)
• π: Giá trị gần bằng 3,14
• r: Bán kính hình cầu
• d: Bán kính hình cầu/bề mặt hình cầu

Lưu ý: Thể tích hình cầu có đơn vị là khối lập phương (m3, cm3,…)

Công thức tính thể tích (V) của hình cầu

Hướng dẫn chi tiết cách tính thể tích hình cầu

Sau đây là các bước tính thể tích hình cầu mà các bạn có thể tham khảo khi giải bài tập:

Bước 1: Viết ra giấy công thức tính V hình cầu

Bây giờ bạn cần viết công thức V = (4 x π xr^3)/ 3 ra giấy để thuận tiện cho việc tính toán chính xác từng thành phần trong công thức.

Hướng dẫn chi tiết cách tính thể tích hình cầu

Bước 2: Đọc kỹ bài toán, tìm bán kính

Tiếp theo, hãy đọc kỹ thông tin được đưa ra trong câu hỏi. Nếu bài toán đã có chiều dài bán kính, hãy tiếp tục viết nó ra giấy. Nhưng nếu bài toán đưa ra đường kính thì mọi người đều có thể sử dụng công thức V = 1/6 x π xd^3. Hoặc các bạn có thể lấy chiều dài đường kính của hình cầu chia cho 2 để tìm bán kính và sử dụng công thức tính thể tích của hình cầu đã ghi ở bước 1.

Nếu bài toán khó hơn và bạn chỉ có dữ liệu về S của hình cầu, bạn sẽ tìm bán kính của hình cầu bằng cách chia S của hình cầu cho 4π. Sau đó bạn lấy kết quả này đưa vào căn bậc hai để tính. Cụ thể, công thức tính bán kính hình cầu theo cách này là: r = √(S/4π).

Bước 3: Tính lũy thừa bậc ba của r

Tiếp theo, tính lũy thừa bậc ba của r bằng cách lấy bán kính và nhân nó với 3 lần, hoặc bạn có thể nâng bán kính lên một số lũy thừa 3.

Ví dụ: (2cm)^3 = 2cm x 2cm x 2cm = 8

(3cm)^3 = 3cm x 3cm x 3cm = 27

Bước 4: Nhân lũy thừa bậc ba của r với 4/3

Sau đó, bạn thay thế kết quả r^3 đã tính thành V = (4 x π xr^3)/ 3 để có công thức nhỏ gọn hơn. Ví dụ: nếu bán kính của hình cầu là 1 cm thì thể tích là V = 4/3 x π x 1 hoặc V = 4/3π

Bước 5: Bạn nhân kết quả trên với số Pi cụ thể

Cuối cùng, đưa số Pi cụ thể vào công thức tính thể tích hình cầu và nhân 3,14 với 4/3. Hoặc bạn luôn có thể đặt số π vào kết quả như V = 4/3π là xong.

Ví dụ: V = 4/3 x 3,14 = 4,19 cm3. Vì vậy kết luận là thể tích của hình cầu có bán kính là 1.

Một số bài toán về thể tích và diện tích hình cầu có lời giải

Ngoài việc học công thức tính V hình cầu các bạn nên học thêm một số bài tập để áp dụng các công thức này.

Bài tập 1

Bài toán: Cho một đường tròn tâm O, chiều dài và bán kính = 9m. Bạn có thể tính S của hình cầu không?

Trả lời: Đầu tiên bạn lấy độ dài bán kính thay công thức tính diện tích hình cầu là 4 x π x R^2 và được:

Diện tích = 4 x 3,14 x 9^2 = 1017,36 (m2)

Bài tập 2

Bài toán: Cho hình tròn tâm O, đường kính = 2,5 cm. Bạn có thể tính S của quả cầu này không?

Trả lời: Để tính S của hình cầu trong bài toán trên, các bạn dùng độ dài đường kính thay công thức tính diện tích hình cầu là π xd^2 và được:

Diện tích = 3,14 x (2,5)^2 = 19,625 (cm2)

Bài tập 3

Bài toán: Cho một hình cầu có đường kính 6cm. Tính diện tích hình cầu?

Trả lời:

Vì d = 6cm nên bán kính của hình cầu = d/2 = 3cm

Vậy S của hình cầu trên là 4 x π x R^2 = 4 x π x 3^2 = 36π (cm2)

Bài tập 4

Câu hỏi: Tính V của một hình cầu có chiều dài và đường kính 4cm?

Trả lời:

r = d/2 = 2cm

Khi đó V của hình cầu = 4/3 x π xr^3 = 4/3 x 3,14 x 2^3 = 33,49 (cm3)

Bài tập 5

Bài toán: Cho một hình cầu có V là 288π cm3. Vậy đường kính của quả cầu là bao nhiêu?

Trả lời:

Vì V = 4/3 x π xr^3 = 288π nên bán kính của hình cầu = 6cm.

Suy ra đường kính = 2r = 2 x 6 = 12 cm

Bài tập 6

Bài toán: Cho 2 quả cầu có đường kính d và chiều dài bằng 1,5cm. Bạn có thể tính V của hình cầu không?

Trả lời:

Đường kính = 1,5cm nên R = 0,75 cm và cụ thể bằng 7,5 x (10)^-3 (m)

Vậy thể tích của hình cầu = 1/3 x π x R^3 = ⅓ x π x (7,5 x 10^-3)^3 = 4,42 x 10^-6 (m3)

Bài tập 7

Câu hỏi: Tính thể tích của hình cầu ngoại tiếp hình lập phương ABCD.EFGH có cạnh dài 3cm?

Trả lời: Gọi bán kính hình cầu ngoại tiếp hình khối R. Như vậy ta có cạnh CE = AB x √3 = 3√3 (cm).

Từ đó suy ra bán kính = 1/2 CE = (3√3)/2 (cm)

Do đó, thể tích hình cầu = V = 4/3 x π x R^3 = 4/3 x π x ((3√3)/2))^3 = (27√3)/2 x π (cm3)

Bài tập 8

Bài toán: Cho hình chóp có tên S.ABC có đáy là tam giác vuông tại A. Cạnh SA ⊥ (ABC) và AB = b, SA = a, AC = c. Chiều dài và bán kính của hình cầu đi qua các hướng S, A, C, B là bao nhiêu?

Trả lời:

Chúng ta gọi trung điểm trên cạnh BC là điểm M. Lúc này MA = MB = MC. Suy ra M là tâm đường tròn ngoại tiếp tam giác ABC như hình vẽ.

Khi đó ta dựng đường thẳng Mt vuông góc với mặt phẳng ABC và ta được Mt song song với cạnh SA và Mt cũng là trục của đường tròn ngoại tiếp tam giác ABC.

Trong mặt phẳng tạo bởi cạnh SA và Mt, đường trung tuyến thuộc SA sẽ cắt đường thẳng Mt tại điểm I. Ta có:

• IA = IS và IC = IB = IA
• Từ đó suy ra IA = IB = IC = IS
• Suy ra I là tâm của hình cầu và được ngoại tiếp trong tứ diện có tên S.ABC.

Khi đó bán kính hình cầu là: R = IA = √AM^2 + MI^2. Trong đó:

• AM = BC/2 = 1/2 √AB^2 + AC^2 = 1/2 √b^2 + c^2
• MI = SA/2 = a/2
• Suy ra bán kính = √((b^2 + c^2)/4) + (a^2/4 ) = 1/2 √a^2 + b^2 + c^2

Một số bài toán tính thể tích, diện tích hình cầu để bạn tự luyện tập

Dưới đây là một số bài tập tự luyện về tính thể tích, diện tích hình cầu mà bạn có thể tham khảo:

Bài 1: Cho hình cầu S bán kính r và hình cầu S' bán kính r'. Biết rằng r' = 2r. Vậy tỷ số diện tích của hình cầu S' và S là bao nhiêu?

1. S = 1/2
2. S = 1/3
3. S = 2
4. S = 4

Bài 2: Cho hình cầu có bán kính r, diện tích S, thể tích V. Vậy công thức nào sau đây sai?

1. S = πr^2
2. S = 4πr^2
3. S = 2πr^2
4. S = 4/3πr^2

Một số dạng toán tính thể tích, diện tích hình cầu để bạn tự luyện tập

Bài 3: Cho hình cầu có bán kính r. Vậy S của hình cầu là gì?

1. S = 4πr^2
2. S = 6πr^2
3. S = 2πr^2
4. S = πr^2

Bài 4: Cho hình cầu có bán kính r. Khi đó chữ V của hình cầu sẽ là gì?

1. S = (4πr^2)/3
2. S = (3πr^3)/4
3. S = (4πr^3)/3
4. S = (2πr^3)/3

Bài 5: Cho tứ diện đều ABCD có cạnh đáy dài a. Tính V của hình cầu ngoại tiếp tứ diện này?

1. (πa^3√6)/8
2. (πa^3√6)/6
3. (πa^3√6)/4
4. (3πa^3√6)/8

Bài viết trên đã chia sẻ chi tiết về hình cầu và công thức tính thể tích, diện tích hình cầu để mọi người cùng học. Hy vọng học sinh sẽ hiểu rõ các công thức trên và cách giải bài tập nhanh chóng. Đây là kiến ​​thức sẽ giúp bạn học hình học tốt hơn trên lớp.

Tham khảo các bài viết liên quan:

• Số nguyên tố là gì? Ví dụ minh họa, tính chất, bảng số nguyên tố
• Tính chất của trọng tâm và cách xác định trọng tâm của tam giác trong Hình học