Tia phân giác là gì? Đường phân giác là gì? Tính chất đường phân giác của tam giác

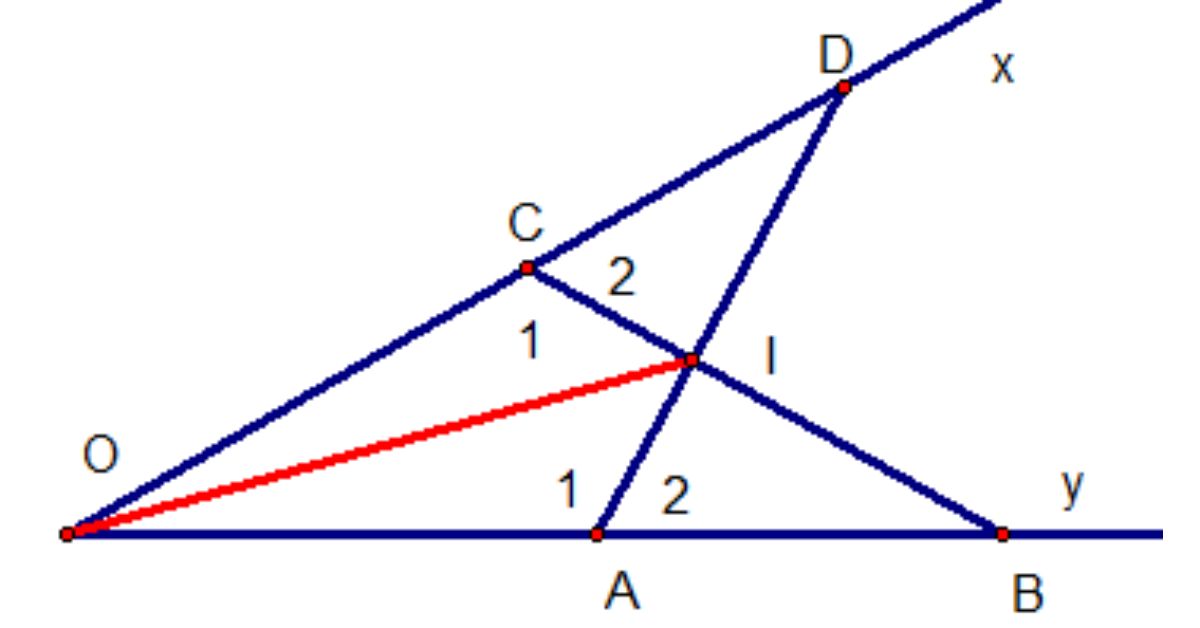
Trong hình học, đường phân giác là một khái niệm quan trọng và quen thuộc, đặc biệt trong việc giải các bài toán về tam giác. Vậy phân giác là gì và làm thế nào để nhận biết và áp dụng trong thực tế? Bài viết này sẽ trả lời những câu hỏi đó và đi sâu vào khám phá đường phân giác cùng với những tính chất đặc biệt của nó trong tam giác. Cùng học để hiểu rõ hơn về vai trò của đường phân giác trong việc chia các góc và nó giúp đơn giản hóa các bài toán phức tạp như thế nào nhé!

Đường phân giác là gì?

Trong hình học, đường phân giác là một khái niệm cơ bản nhưng cực kỳ quan trọng, đặc biệt khi giải các bài toán về góc và tam giác. Tia phân giác của một góc là tia xuất phát từ đỉnh của góc đó và chia góc đó thành hai phần có độ lớn bằng nhau. Nghĩa là, nếu trong tam giác ABC có một góc thì đường phân giác xuất phát từ đỉnh B và đi qua một điểm D nào đó trên cạnh của góc, tạo thành hai góc ABD và DBC có độ lớn bằng nhau.

Tính chất của tia phân giác

• Độ chính xác: Tia phân giác chia góc ban đầu thành hai góc bằng nhau một cách chính xác, rất hữu ích trong tính toán và vẽ.
• Vai trò trong tam giác: Trong một tam giác, ba đường phân giác (nối từ đỉnh sang cạnh đối diện) luôn cắt nhau tại một điểm đặc biệt gọi là tâm của đường tròn nội tiếp. Đây là điểm mà từ đó một đường tròn có thể được vẽ tiếp tuyến với tất cả các cạnh của tam giác.

Cách nhận biết và vẽ đường phân giác

Vì vậy, bạn biết phân giác là gì. Tia phân giác của một góc là tia xuất phát từ đỉnh của góc và chia góc đó thành hai phần bằng nhau.

Đường phân giác tạo hai góc con bằng nhau, nghĩa là nếu bạn có góc ∠ABC thì đường phân giác sẽ chia góc này thành hai góc con ∠ABD và ∠DBC sao cho: ∠ABD=∠DBC.

Cách vẽ tia phân giác của một góc:

Bước 1: Vẽ một góc Lấy điểm B làm đỉnh của góc và vẽ hai cạnh của góc, ví dụ BA và BC.

Bước 2: Dùng dụng cụ đo góc (thước đo góc) hoặc phần mềm vẽ hình học để đo kích thước góc ∠ABC. Hãy nhớ kích thước này hoặc lưu nó để so sánh sau.

Bước 3: Xác định điểm phân giác. Đặt thước hoặc phần mềm vẽ hình học sao cho chia góc ∠ABC thành hai góc bằng nhau. Đo và đánh dấu một điểm trên cạnh của góc sao cho hai phần của góc có kích thước bằng nhau.

Bước 4: Vẽ một tia từ đỉnh góc qua điểm bạn đã đánh dấu. Tia này là tia phân giác, chia góc ∠ABC thành hai góc con bằng nhau.

Bước 5: Kiểm tra lại. Đảm bảo rằng hai góc con được tạo bởi đường phân giác bằng nhau bằng cách sử dụng lại thước đo góc.

Đường phân giác là gì?

Ngoài việc cần tìm hiểu thế nào là đường phân giác, chúng ta cũng cần hiểu khái niệm đường phân giác trong một tam giác. Là đoạn thẳng nối một đỉnh của một tam giác với giao điểm của đường phân giác của góc đó với cạnh đối diện của tam giác đó.

Cụ thể, đường thẳng/đường phân giác chia góc ở đỉnh của tam giác thành hai góc bằng nhau. Đoạn thẳng này không chỉ chia góc thành hai phần bằng nhau mà còn chia cạnh đối diện với tam giác thành hai phần tỉ lệ với các cạnh còn lại của tam giác.

Định nghĩa: Đường phân giác của một tam giác là đoạn thẳng xuất phát từ một đỉnh và chia góc tại đỉnh đó thành hai góc bằng nhau. Đồng thời, nó cắt cạnh đối diện tại điểm mà tại đó tỉ số giữa các đoạn của cạnh đối diện bằng tỉ số giữa các cạnh còn lại của tam giác.

Đoán và vẽ đường nối từ đỉnh của góc đến cạnh đối diện sao cho góc đó chia góc đó thành hai góc bằng nhau. Kiểm tra tỷ lệ của các đoạn ở phía đối diện để xác nhận rằng chúng tỷ lệ với các cạnh còn lại của tam giác.

Các tính chất chính của đường phân giác

Chia một góc thành hai phần bằng nhau: Tính chất nổi bật nhất của đường phân giác là gì? Là khả năng chia góc ở đỉnh của một tam giác thành hai góc bằng nhau. Khi đã biết về đường phân giác, đường phân giác, bạn có thể dễ dàng chứng minh các góc con do đường phân giác tạo ra bằng nhau, từ đó giúp nhận biết và giải các bài toán liên quan đến các góc trong tam giác. giác quan.

Tính tỉ lệ các cạnh đối diện: Đường phân giác chia cạnh đối diện của tam giác thành hai đoạn có tỉ lệ các cạnh còn lại bằng nhau. Cụ thể, nếu đường phân giác cắt cạnh đối diện tại điểm D thì tỉ số giữa các đoạn thẳng BD và DC bằng tỉ số hai cạnh còn lại của tam giác. Điều này có thể được biểu thị bằng công thức: AC/AB = DC/BD.

Giao điểm của các đường phân giác: Trong một tam giác, ba đường phân giác cắt nhau tại một điểm đặc biệt gọi là tâm của đường tròn nội tiếp. Tâm này là điểm mà từ đó bạn có thể vẽ một đường tròn tiếp xúc với tất cả các cạnh của tam giác.

Áp dụng tính chất của đường phân giác

Chứng minh định lý: Tính chất đường phân giác được dùng để chứng minh nhiều định lý trong hình học, chẳng hạn như định lý về tỉ số hai cạnh đối diện và các bài toán liên quan đến góc trong tam giác.

Giải bài toán: Trong các bài toán về tam giác, đặc biệt khi cần tính tỉ lệ các đoạn thẳng và các góc, việc hiểu rõ tính chất của đường phân giác giúp bạn giải bài toán một cách chính xác và hiệu quả.

Thiết kế kiến ​​trúc: Hiểu được tính chất của đường phân giác cũng có thể được áp dụng trong thiết kế kiến ​​trúc để tạo ra các cấu trúc đối xứng và cân đối.

Ví dụ minh họa: Cho tam giác ABC có đường phân giác AD. Đường phân giác AD chia góc ∠BAC thành hai góc bằng nhau và chia cạnh đối diện BC thành hai đoạn BD và DC theo tỉ lệ: AC/AB = DC/BD.

Điều này chứng tỏ các đoạn thẳng BD và DC chia cạnh BC tỉ lệ với các cạnh AB và AC, cho phép tính độ dài và góc một cách chính xác.

Sự khác biệt giữa phân giác và phân giác

Bisector và bisector thường bị nhầm lẫn nhưng chúng có sự khác biệt rõ ràng:

Tia phân giác: Tia xuất phát từ đỉnh của một góc và chia góc đó thành hai góc bằng nhau. Đường phân giác không phải là đoạn thẳng có độ dài nhất định mà là một phần của đường thẳng vô hạn.

Đường phân giác: Trong một tam giác, đường phân giác là đoạn thẳng nối một đỉnh của tam giác với điểm mà đường phân giác cắt cạnh đối diện. Đường phân giác là một đoạn thẳng có độ dài xác định và chia cạnh đối diện của tam giác theo một tỷ lệ nhất định.

Mối quan hệ: Đường phân giác là phần tử cơ bản có thể được sử dụng để xác định đường phân giác. Đường phân giác chính là đoạn đường có đường phân giác cắt cạnh đối diện của tam giác và chia cạnh đối diện thành hai phần tương ứng.

Ứng dụng của tia phân giác

Đường phân giác không chỉ là khái niệm cơ bản trong hình học mà còn có nhiều ứng dụng thực tế trong toán học và các lĩnh vực khác của đời sống. Vậy ứng dụng của đường phân giác là gì? Hãy cùng khám phá một số ứng dụng quan trọng dưới đây.

Ứng dụng giải các bài toán hình học về đường phân giác

Trong toán học, đặc biệt là hình học, việc sử dụng đường phân giác có thể giải các bài toán liên quan đến góc và hình tam giác.

Chứng minh tính chất của góc: Phân giác được dùng để chứng minh hai góc bằng nhau hoặc tìm góc trong các bài toán hình học phức tạp. Ví dụ, trong một tam giác, nếu một đường phân giác của một góc chia một góc thành hai phần bằng nhau thì có thể dùng để chứng minh hai đoạn thẳng đối diện cũng có một tỷ lệ nhất định, thông qua định lý đường phân giác.

Xác định tâm của đường tròn nội tiếp: Trong một tam giác, ba đường phân giác của các góc sẽ cắt nhau tại một điểm gọi là tâm của đường tròn nội tiếp. Điểm này rất quan trọng trong việc xác định vị trí và kích thước của đường tròn nội tiếp của tam giác, giúp việc tính toán dễ dàng hơn trong các bài toán liên quan đến diện tích và chu vi.

Giải bài toán đối xứng: Đường phân giác thường được sử dụng để tạo các bài toán đối xứng trong hình học.

Ứng dụng trong kiến ​​trúc và kỹ thuật tia phân giác

Ngoài toán học, đường phân giác còn có nhiều ứng dụng trong kiến ​​trúc và kỹ thuật:

Thiết kế kiến ​​trúc: Tia chia đôi được sử dụng trong thiết kế kiến ​​trúc để tạo ra những kết cấu đối xứng và cân đối. Việc áp dụng đường phân giác giúp kiến ​​trúc sư đảm bảo các góc, cạnh được phân chia chính xác, từ đó tạo nên những công trình có tính thẩm mỹ cao.

Kỹ thuật cơ khí: Trong kỹ thuật cơ khí, tia phân giác có ứng dụng gì? Tia phân giác có thể được sử dụng để đảm bảo độ chính xác trong việc lắp ráp các chi tiết máy. Điều này giúp cải thiện hiệu suất và độ bền của các thiết bị cơ khí.

Thiết kế sản phẩm: Trong thiết kế sản phẩm, đường phân giác giúp người thiết kế tạo ra những sản phẩm có tính thẩm mỹ và công năng tốt hơn, đặc biệt trong việc phân chia không gian hay tạo các góc cân đối. .

Ứng dụng trong đời sống của tia phân giác

Đường phân giác cũng xuất hiện trong nhiều tình huống hàng ngày mà có thể chúng ta không để ý:

Trang trí nội thất: Trong trang trí nội thất, tia phân giác có ứng dụng gì? Tia này giúp tạo nên những không gian cân bằng và hài hòa. Điều này có thể thấy rõ trong việc sắp xếp nội thất để không gian sống trở nên tiện nghi và đẹp mắt hơn.

Thiết kế đồ họa: Đường phân giác được sử dụng trong thiết kế đồ họa để tạo ra các tác phẩm nghệ thuật đối xứng và cân đối, từ logo đến áp phích.

Giáo dục: Trong dạy học toán, đường phân giác có thể được sử dụng như một công cụ để giải thích các khái niệm hình học cho học sinh, giúp các em hiểu rõ hơn về các nguyên lý, định lý trong toán học.

Câu hỏi thường gặp – Câu hỏi thường gặp về đường phân giác

Làm thế nào để kiểm tra xem đường phân giác có đúng không?

Để kiểm tra tia phân giác, bạn có thể:

• Sử dụng thước đo góc để xác nhận rằng các góc con được tạo thành bằng nhau.
• Kiểm tra tỷ lệ giữa các đoạn ở các cạnh đối diện để đảm bảo chúng tỷ lệ với các cạnh còn lại của tam giác.

Tại sao hiểu biết về phân giác lại quan trọng?

Hiểu rõ đường phân giác, đường phân giác là gì sẽ giúp bạn giải các bài toán hình học một cách hiệu quả và áp dụng các tính chất hình học trong thực tế, từ thiết kế kiến ​​trúc đến phân tích kỹ thuật.

Những công cụ nào có thể giúp vẽ đường phân giác chính xác?

Để vẽ đường phân giác chính xác, bạn có thể sử dụng:

• Thước đo góc và compa để đo và chia góc.
• Phần mềm vẽ hình học như GeoGebra hoặc AutoCAD để có độ chính xác cao hơn.
• Công cụ vẽ hình học chuyên dụng trong bộ dụng cụ học tập.

Đường phân giác của góc có ảnh hưởng đến các tính chất khác của tam giác không?

Có, đường phân giác có ảnh hưởng đến các tính chất khác của tam giác, chẳng hạn như:

• Nó có thể được sử dụng để tính các điểm đặc biệt như điểm giữa của đường tròn nội tiếp.
• Đường phân giác cũng giúp xác định tỷ lệ và các tính chất khác của hình tam giác trong các bài toán hình học.

Phần kết luận

Trong hình học, đường phân giác là gì? Đây là một khái niệm cơ bản nhưng cần thiết để có thể giải các bài toán liên quan đến góc và hình tam giác. Được sử dụng rộng rãi không chỉ trong toán học mà còn trong nhiều lĩnh vực như kiến ​​trúc, kỹ thuật và thiết kế, đường phân giác giúp đơn giản hóa các vấn đề phức tạp và tạo ra các cấu trúc đối xứng, chính xác.

Bài viết này đã cung cấp cái nhìn tổng quan về đường phân giác, cách nhận biết và vẽ chúng, cùng với những ứng dụng thực tế và sự khác biệt giữa đường phân giác và đường phân giác. Hy vọng các bạn đã có cái nhìn rõ ràng về vai trò của đường phân giác trong hình học và cách nó giúp giải các bài toán hình học một cách hiệu quả.

Để nắm vững các khái niệm và kỹ thuật liên quan, đừng quên luyện tập vẽ và áp dụng đường phân giác vào các bài toán thực tế. Điều này không chỉ nâng cao khả năng giải quyết vấn đề mà còn mở rộng khả năng ứng dụng trong mọi lĩnh vực của đời sống.

Xem thêm:

• Số hữu tỉ là gì? Số vô tỷ là gì? Đặc điểm của các con số trong Toán học
• Bộ công thức Hoán vị – Hợp quy – Tổ hợp đầy đủ nhất trong Toán học