Tính diện tích xung quanh hình nón, diện tích toàn phần, thể tích hình nón

Công thức tính thể tích, diện tích toàn phần diện tích xung quanh hình nón thực sự được sử dụng phổ biến trong toán học. Vì về cơ bản, hình nón vốn được tạo ra bằng cách xoay một tam giác vuông. Vì vậy, công thức này cũng được coi là một trong những công thức cơ bản nhất dành cho những ai muốn thành thạo lĩnh vực tính toán. Nếu muốn tham khảo chi tiết các công thức tính hình nón hãy đọc ngay gợi ý từ Thác Trầm Hương Mobile trong nội dung dưới đây.

hình nón là gì?

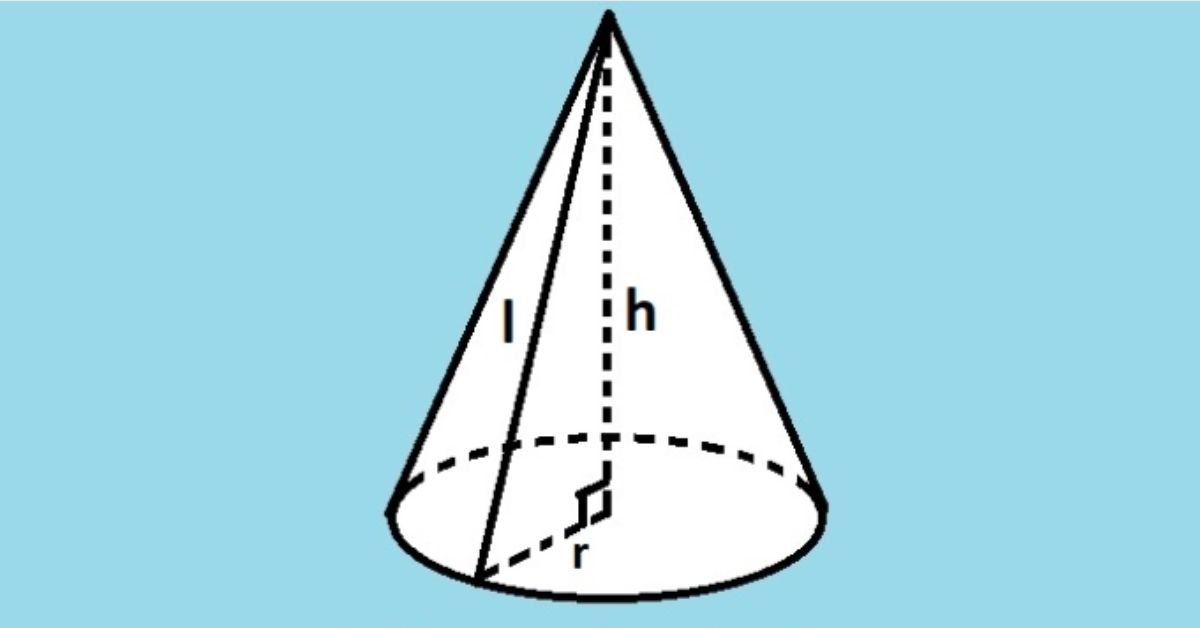
Trong toán học, hình nón là một vật thể hình học không gian có hình dạng giống như một chiếc mũ thực sự. Điểm đặc biệt của loại hình học này là chúng được xây dựng với phần trên nhọn và hình tròn ở phía dưới dựa trên phối cảnh 3 chiều đặc biệt. Trong đó, hình nón thường được xác định bởi 3 yếu tố chính gồm bán kính đáy (hình tròn ở đáy), chiều cao và đỉnh.

Theo đó, các yếu tố trên sẽ quyết định hình dạng, kích thước của hình nón. Tuy nhiên, để nắm được cách tính diện tích xung quanh hình nón, trước hết bạn phải hiểu ý nghĩa của từng hệ số thông qua các thông số sau:

• Bán kính cơ sở (r): Đây là khoảng cách từ tâm của cơ sở đến bất kỳ điểm nào trên đường tròn ở cơ sở.
• Chiều cao (h): Chiều dài từ đỉnh hình nón đến mặt phẳng chứa đường tròn ở đáy.
• Đỉnh (V): Đây là điểm tập trung của hình nón, nơi tất cả các đoạn thẳng từ đỉnh đến các điểm trên đường tròn ở đáy hội tụ lại.

Nhìn chung, công thức tính diện tích xung quanh, diện tích tổng và thể tích hình nón sẽ thường được áp dụng để mô tả, tính toán trong nhiều lĩnh vực xây dựng và thiết kế trong thực tế. Vì vậy, nếu muốn học cách tính và các bài tập liên quan đến hình nón, bạn đọc nên tham khảo nội dung trình bày dưới đây.

Cách tính chính xác diện tích xung quanh hình nón

Tính diện tích xung quanh hình nón cực kỳ đơn giản. Bạn có thể áp dụng thành công phép tính này ngay lần đầu thông qua những gợi ý dưới đây.

Công thức tính diện tích xung quanh hình nón

Diện tích xung quanh của hình nón là tổng diện tích của tất cả các bề mặt ngoại trừ đáy. Để tính diện tích xung quanh (S), chúng ta thường sử dụng công thức sau:

Trong đó:

• Sxq là ký hiệu cho khu vực xung quanh.
• π là một hằng số trong toán học, chúng được định nghĩa xấp xỉ bằng 3,14.
• r là bán kính đáy hình nón.
• l là đoạn thẳng gọi là đường sinh, nối đỉnh hình nón với điểm trên đường tròn ở đáy. Để tính l, bạn có thể sử dụng định lý Pythagore với công thức bằng căn bậc hai của tổng bình phương của r và h, trong đó h là độ cao của hình nón.

Ví dụ minh họa: Xét một hình nón có bán kính đáy r = 5 và chiều cao ℎ = 8. Tính diện tích xung quanh hình nón trong bài toán trên.

Giải thích chi tiết:

• Theo bài toán, ta tính được l = (r)2 +(h)2 = (5)2+(8)2 = 89
• Như vậy diện tích xung quanh hình nón trong bài toán này sẽ bằng, Sxq = π xrxl = π x 5 x 89 = 148

Ứng dụng tính diện tích xung quanh hình nón

Trong thực tế, việc tính diện tích xung quanh hình nón được áp dụng trong các lĩnh vực sau:

Sản xuất và xây dựng: Trong xây dựng cột, tháp nhà ở hay kết cấu hình nón, công thức tính diện tích xung quanh giúp xác định lượng vật liệu cần thiết để phủ và hoàn thiện bề mặt bên ngoài của kết cấu. Ngay cả khi áp dụng phép tính này, bạn có thể tính toán được vật liệu cần thiết để xây dựng và thiết kế dự án.

Ngành công nghiệp: Trong thiết kế bao bì có dạng hình nón, việc áp dụng công thức tính diện tích xung quanh giúp nhà sản xuất ước tính được nguyên liệu cần thiết để sản xuất bao bì theo yêu cầu. Chúng thậm chí còn giúp bạn tính toán chính xác không gian lưu trữ sản phẩm trong trường hợp này.

Trong giáo dục: Công thức tính diện tích xung quanh hình nón thường xuất hiện trong các bài toán và trong các đề thi. Điều này giúp học sinh, sinh viên nắm được những kiến ​​thức cơ bản của toán học để áp dụng vào thực tế.

Cách tính chính xác tổng diện tích hình nón

Trên thực tế, công thức tính diện tích toàn phần của hình nón dựa trên phương pháp tính diện tích xung quanh. Bạn có thể tham khảo nội dung chúng tôi gợi ý dưới đây để nắm được công thức và phương pháp tính của loại đặc biệt này.

Công thức tính diện tích toàn phần của hình nón

Tổng diện tích của hình nón bao gồm diện tích xung quanh hình nón và diện tích đáy. Để tính tổng diện tích (Stp), chúng ta sẽ sử dụng công thức sau:

Trong đó:

• Stp là ký hiệu cho tổng diện tích của hình nón.
• Sxq là diện tích xung quanh. Công thức này đã được hướng dẫn cụ thể ở trên.
• π là một hằng số trong toán học, chúng được định nghĩa xấp xỉ bằng 3,14.
• r là bán kính đáy hình nón.

Ghi chú: Diện tích xung quanh hình nón chỉ là công thức tính phần bên ngoài của hình nón, còn tổng diện tích bao gồm cả diện tích xung quanh và đáy. Vì vậy, bạn cần chú ý sử dụng chính xác công thức của 2 cách tính này để có được kết quả chính xác nhất.

Ví dụ minh họa: Giả sử chúng ta có một hình nón có bán kính đáy r = 6 và chiều cao h = 10. Tính tổng diện tích của hình nón trên.

Giải thích chi tiết:

• Dựa trên dữ liệu đã cho, chúng ta có l = l = (r)2 +( h)2 = (6)2+(10)2 = 136
• Từ đó ta có thể tính diện tích xung quanh hình nón như sau: Sxq = π xrxl = π x 6 x 136 = 220
• Như vậy, tổng diện tích của hình nón trên sẽ là Stp = Sxq + π x (r)2= 333

Ứng dụng tính diện tích toàn phần của hình nón

Tính tổng diện tích hình nón có vai trò quan trọng trong nhiều lĩnh vực của đời sống. Cụ thể, trong kiến ​​trúc và xây dựng, việc tính tổng diện tích của cột hình nón giúp xác định lượng vật liệu cần thiết để hoàn thiện cả bề mặt xung quanh và mặt trên. Như vậy, khi thiết kế đài phun nước hình nón, tổng diện tích sẽ quyết định lượng sơn hoặc vật liệu trang trí cần sử dụng.

Trong lĩnh vực công nghiệp, việc tính toán tổng diện tích rất quan trọng trong việc sản xuất thùng chứa hình nón. Việc xác định diện tích bề mặt cần xử lý, phủ giúp đảm bảo chất lượng và độ an toàn của container. Đặc biệt là khi nó liên quan đến các thành phần như hóa chất hoặc dầu. Ngay cả trong ngành in 3D, tổng diện tích của hình nón cũng ảnh hưởng đến lượng vật liệu cần thiết để tạo ra sản phẩm. Điều này làm cho công thức này trở nên quan trọng trong quá trình sản xuất.

Ngoài ra, công thức tính diện tích toàn phần của hình nón còn có ứng dụng trong giáo dục và nghiên cứu trong thực tế đời sống. Công thức này và cách tính diện tích xung quanh hình nón cũng thường xuất hiện trong các bài toán. Điều này giúp học sinh nắm vững kiến ​​thức, kỹ năng toán học cơ bản ngay từ khi còn đi học.

Cách đơn giản để tính chính xác thể tích hình nón

Khác với công thức tính diện tích xung quanh hình nón, cách tính thể tích của hình học không gian này nhìn chung sẽ có phần đặc biệt hơn. Cụ thể như sau:

Công thức tính thể tích hình nón

Thể tích của hình nón là không gian mà hình học này chiếm giữ. Vì vậy, để tính thể tích hình nón, người dùng phải áp dụng công thức đặc biệt sau:

Trong đó:

• V là ký hiệu công thức tính thể tích hình nón
• π là một hằng số trong toán học, chúng được định nghĩa xấp xỉ bằng 3,14.
• r và h lần lượt là bán kính đáy và chiều cao của hình nón.

Ví dụ minh họa: Giả sử bài toán cho một hình nón có bán kính đáy r = 4 và chiều cao h = 9. Hãy tính thể tích và tổng diện tích của hình nón trên.

Giải thích chi tiết:

• Theo bài toán, ta tính được l = (r)2 +(h)2 = (4)2+(9)2 = 97
• Diện tích xung quanh hình trụ là Sxq = π xrxl = π x 4 x 97 = 124
• Từ đó ta tính được tổng diện tích hình nón như sau: Stp = Sxq + π x (r)2= 174
• Vậy thể tích của tụ điện cần tìm là V = 13π x r2 xh = 48π

Ứng dụng tính thể tích hình nón

Tính thể tích hình nón không chỉ là một khái niệm toán học trừu tượng mà còn có ứng dụng rộng rãi và thực tiễn trong nhiều lĩnh vực của đời sống. Cụ thể, trong quản lý dung lượng và lưu trữ, tính toán thể tích giúp dự đoán và quản lý lưu trữ, từ container hàng hóa đến bồn chứa nước lớn. Điều này giúp người dùng tiết kiệm công sức và tối ưu hóa thời gian trong khi thực hiện công việc.

Trong ngành sản xuất và đóng gói, thể tích hình nón được coi là công thức quan trọng trong việc xác định lượng vật liệu cần thiết để thiết kế bao bì, chai lọ hay thậm chí là đóng gói sản phẩm trong thùng chứa. có hình nón. Điều này giúp tối ưu hóa không gian lưu trữ sản phẩm và tài nguyên xử lý. Ngay cả công thức tính thể tích hình nón cũng thường xuất hiện trong các bài toán, đề thi. Điều này giúp học sinh, sinh viên hiểu sâu hơn về cách áp dụng kiến ​​thức đã học vào thực tế.

Phần kết luận

Nói chung, cách tính thể tích và diện tích của một thành phố và diện tích xung quanh hình nón khá đơn giản. Ngay cả công thức thực hiện phép tính cũng dễ nhớ và dễ hiểu. Nếu không nhớ công thức thì chỉ cần xem lại gợi ý Thác Trầm Hương Mobile đã trình bày ở trên. Thậm chí, hãy để lại bình luận bên dưới nếu bạn gặp vấn đề trong khi theo dõi bài viết để nhận được câu trả lời cụ thể hơn nhé!

XEM THÊM

• Cách tính diện tích hình thang & hình thang vuông, bài tập thực hành minh họa chi tiết
• Số thực là gì? Một số dạng toán phổ biến của số thực
• Công thức tính diện tích hình vuông chính xác nhất