Trọng tâm là gì? Trọng tâm của tam giác thường, vuông, cân…

Bạn đang tìm kiếm thông tin về trọng tâm là gì? Trọng tâm của tam giác là gì? và các thông tin liên quan khác. Trong bài viết này Fresh Lemon Review sẽ chia sẻ đến các bạn những kiến thức, vấn đề quan trọng nhất. Đặc biệt, quy tắc trung tâm các dạng tam giác vuông, tam giác cân, tam giác đều,… vô cùng thú vị. Xem ngay!
Định nghĩa của focus là gì?
 Điều gì được hiểu là tập trung?
Điều gì được hiểu là tập trung?
Trọng tâm là gì?
Bạn có biết trọng tâm là gì không? Trọng tâm là điểm mà tại đó khi bạn đặt một hình trụ thẳng đứng, vật có khả năng giữ thăng bằng. Khái niệm này không chỉ được áp dụng trong bối cảnh vật lý mà còn mở rộng sang các khía cạnh của cuộc sống hàng ngày, có thể hiểu theo cả nghĩa đen và nghĩa bóng.
Trong mọi bối cảnh, trọng tâm là điểm trung tâm, trung tâm quan trọng của một đối tượng hoặc một vấn đề. Trong lĩnh vực toán học, trọng tâm thường được sử dụng để mô tả vị trí trung tâm của các hình hình học, chẳng hạn như trọng tâm của một hình tam giác, trọng tâm của một hình chữ nhật hoặc trọng tâm của một tứ giác.
Định nghĩa trọng tâm theo từ điển
Danh từ trung tâm có 3 ngữ nghĩa sau:
- (Vật lý) Điểm mà tại đó trọng lực tác dụng lên một vật.
- (Toán học) Giao điểm của ba đường trung tuyến trong một tam giác.
- Điểm quan trọng nhất. Ví dụ: Đây là trọng tâm của vấn đề.
XEM SHOP CHUYÊN DỤNG CỤ HỌC TẬP UY TÍN TẠI ĐÂY
Trọng tâm của tam giác là gì?
Vậy trong một tam giác, trung điểm là gì? Trọng tâm của một tam giác là giao điểm của ba đường trung tuyến tương ứng.
Đường trung bình của tam giác là đoạn thẳng nối đỉnh của tam giác với trung điểm của cạnh đối diện.
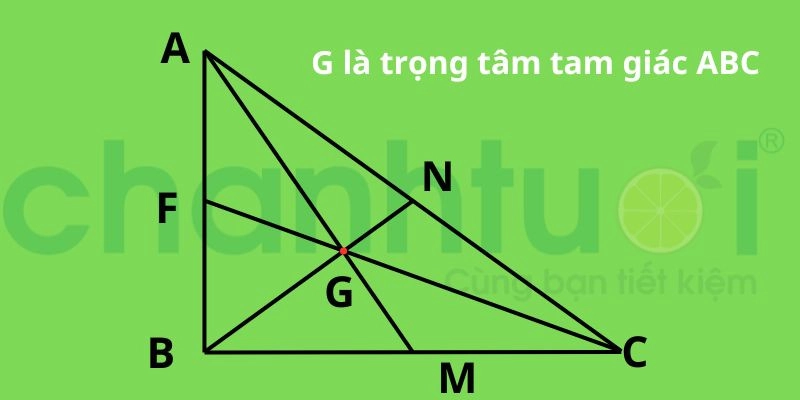 Giao điểm của ba đường trung tuyến là trọng tâm của tam giác
Giao điểm của ba đường trung tuyến là trọng tâm của tam giác
Ví dụ: Trong tam giác ABC, các đường trung tuyến AM, BN, CP xuất phát từ các đỉnh A, B, C và cắt nhau tại một điểm chung G.
Do đó, trọng tâm của tam giác ABC là điểm G, tại đó ba đường trung tuyến AM, BN, CP cắt nhau.
Một tam giác có bao nhiêu trọng tâm?
Một tam giác chỉ có một trọng tâm. Tâm của tam giác là giao điểm của ba đường trung tuyến. Đường trung bình của một tam giác là đoạn thẳng nối đỉnh của tam giác với trung điểm của cạnh đối diện. Trên đồ thị tam giác, trọng tâm là giao điểm của ba đường trung tuyến và nằm bên trong tam giác.
Tính chất trọng tâm của tam giác
Tính chất quan trọng của trọng tâm tam giác: Khoảng cách từ trọng tâm đến ba đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
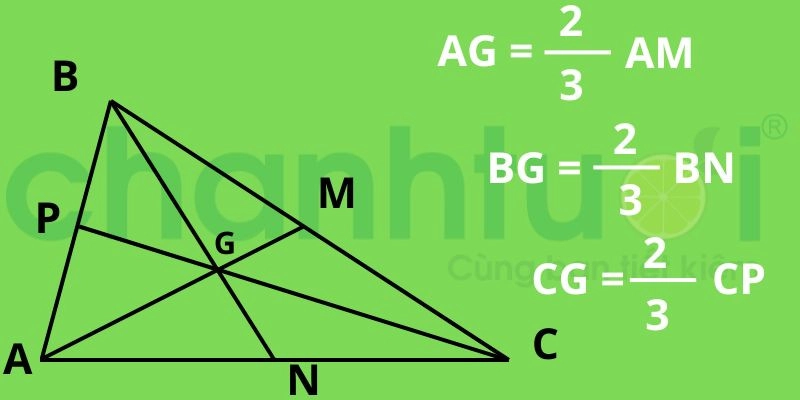 Tính chất đường tâm của tam giác
Tính chất đường tâm của tam giác
Giả sử tam giác ABC có 3 đường trung tuyến AM, BN, CP với G là trọng tâm như hình vẽ. Theo tính chất trên ta có:
- GA = 2/3 sáng
- GB = 2/3 AN
- GC = 2/3 CP
Ngoài ra, ta còn một số hằng số khác liên quan đến trọng tâm của tam giác. Về mặt phối cảnh, điểm G chia mỗi đường trung tuyến thành 3 phần bằng nhau.
- Xét đường trung tuyến AM, ta có: AM = 3 GM; AM = 3/2 AG; AG = 2 GM; GM = 1/2 AG,…
- Đối với đường trung tuyến BN, ta có: BN = 3 GN; BN = 3/2 BG; BG = 2GN; GN = 1/2 BG,…
- Đối với đường trung tuyến CP, ta có: CP = 3 GP; CP = 3/2 CG; CG = 2 GP; GP = 1/2 CG,…
MUA BỘ QUY TẮC, ĐO BẰNG ĐỘ, SINH VIÊN EKE TẠI ĐÂY
Quy tắc tâm tam giác theo vectơ
Tâm của tam giác là giao điểm của ba đường trung tuyến. Áp dụng quy tắc trọng tâm tam giác:
Điểm G là trọng tâm tam giác ABC nên ta có:
- (GA) ⃗+(GB) ⃗+(GC) ⃗=(0) ⃗
- (MA) ⃗+(MB) ⃗+(MC) ⃗= 3(MG) ⃗ với mọi điểm M tùy ý.
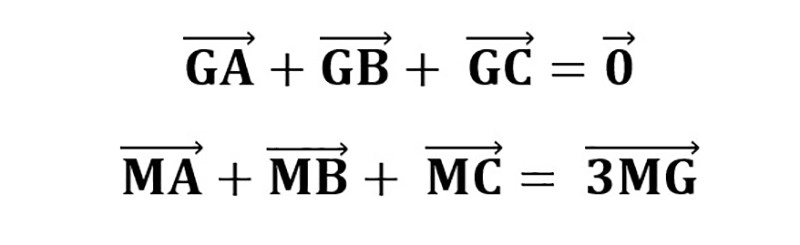 Khi điểm G là trọng tâm tam giác ABC
Khi điểm G là trọng tâm tam giác ABC
Với mỗi loại tam giác đặc biệt, tính chất tâm của tam giác được biểu diễn như sau:
1. Trọng tâm của tam giác vuông
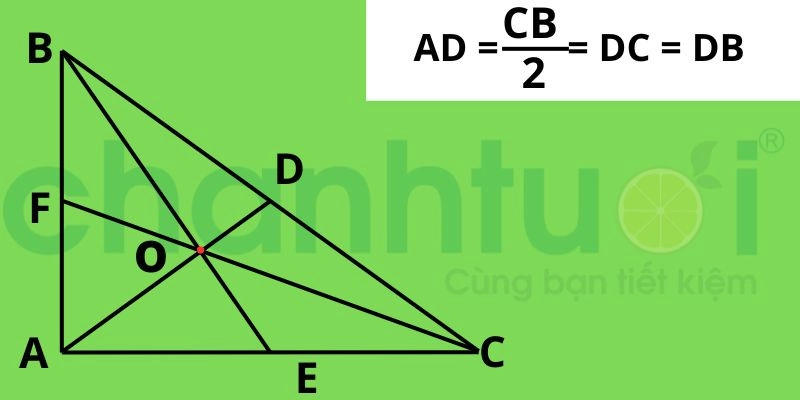 Tính chất trung tâm của tam giác vuông
Tính chất trung tâm của tam giác vuông
Giả sử tam giác ABC vuông tại A. 3 đường trung tuyến AD, BE, CF cắt nhau tại trọng tâm O. Ta có AD là đường trung bình của góc vuông CAB nên AD = 1/2 CB = DC = DB.
2. Trọng tâm của tam giác cân
Giả sử tam giác ABC cân tại A, lấy O là trọng tâm. Vì tam giác ABC cân tại A nên AO vừa là đường trung tuyến, đường cao, vừa là đường phân giác.
Do đó, ta có thể suy ra hệ quả trọng tâm của tam giác cân ABC như sau:
- Góc BAD bằng góc CAD.
- Đường trung tuyến AD vuông góc với cạnh đáy BC.
3. Trọng tâm của tam giác vuông cân
Giả sử tam giác ABC vuông tại A và O là trọng tâm. AM là đường trung trực, đường cao và đường trung trực của tam giác này nên AM vuông góc với BC. Mặt khác, vì tam giác ABC vuông tại A nên ta suy ra:
- AB = AC => BP = CN và BN = AN = CP = AP.
4. Trọng tâm của tam giác đều
Cho tam giác đều ABC, G là giao điểm của ba đường trung tuyến, đường cao và đường phân giác.
Theo tính chất của tam giác đều, ta có G là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp tam giác ABC.
5. Trọng tâm của tam giác tứ diện
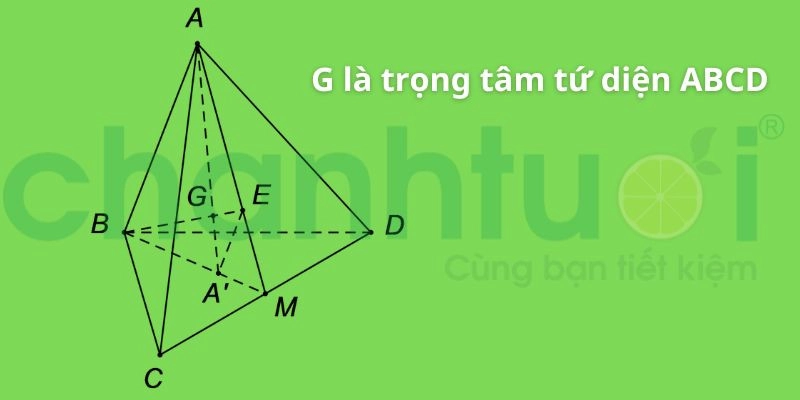 Trọng tâm của tam giác tứ diện
Trọng tâm của tam giác tứ diện
- Gọi G là trọng tâm của tứ diện ABCD.
- Trọng tâm của tứ diện là giao điểm của bốn đường thẳng nối đỉnh và trọng tâm của tam giác đối diện.
Cách xác định trọng tâm của tam giác
Có hai cách chính để xác định trọng tâm của tam giác ABC, dựa vào tính chất của trọng tâm của tam giác:
Cách 1: Sử dụng định nghĩa trọng tâm là giao điểm của ba đường trung tuyến.
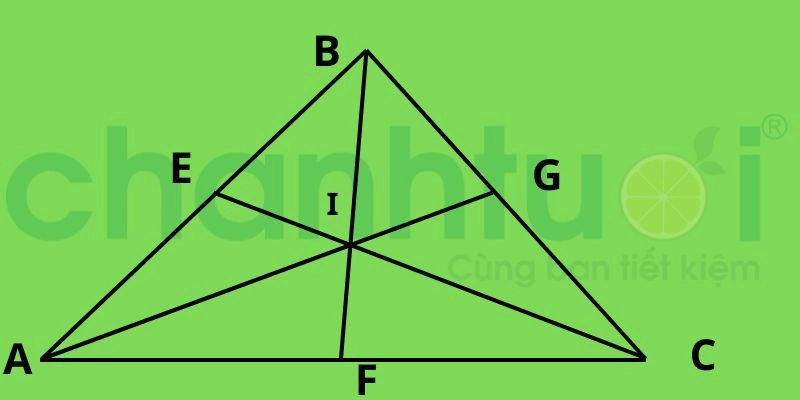 Trọng tâm I của tam giác ABC
Trọng tâm I của tam giác ABC
- Bước 1: Vẽ tam giác ABC và xác định trung điểm các cạnh AB, BC, CA.
- Bước 2: Nối các đỉnh A, B, C với các trung điểm tương ứng tạo thành ba đường trung tuyến AG, BF, CE.
- Bước 3: Giao điểm I của ba đường trung tuyến AG, BF, CE là trọng tâm của tam giác ABC.
Cách 2: Sử dụng tính chất tỉ lệ trên đường trung tuyến.
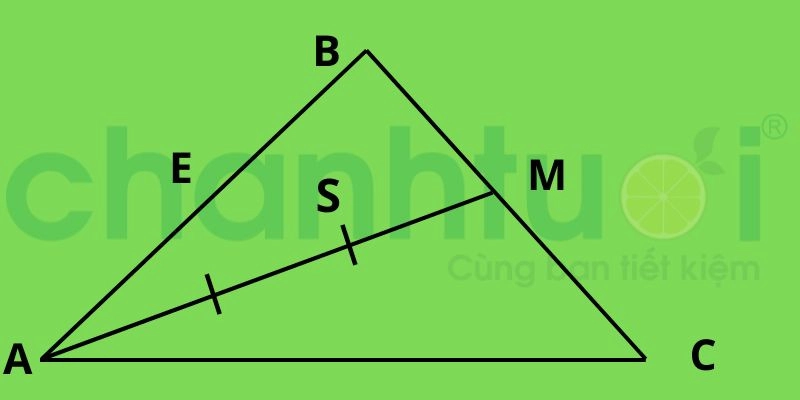 Xác định trọng tâm S của trọng tâm
Xác định trọng tâm S của trọng tâm
- Bước 1: Vẽ tam giác ABC và xác định trung điểm M của cạnh BC.
- Bước 2: Nối đỉnh A với trung điểm M rồi lấy điểm S sao cho AS = 2/3 AM. Theo tính chất trọng tâm của tam giác, điểm S là trọng tâm của tam giác ABC.
Công thức tính trọng tâm của tam giác
Công thức tính độ dài đường tâm của tam giác
Khoảng cách từ trọng tâm của tam giác đến một đỉnh bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
Ví dụ: Đường trung tuyến AM = 3cm thì khoảng cách từ trọng tâm G đến đỉnh A = ⅔ độ dài AM = 2cm.
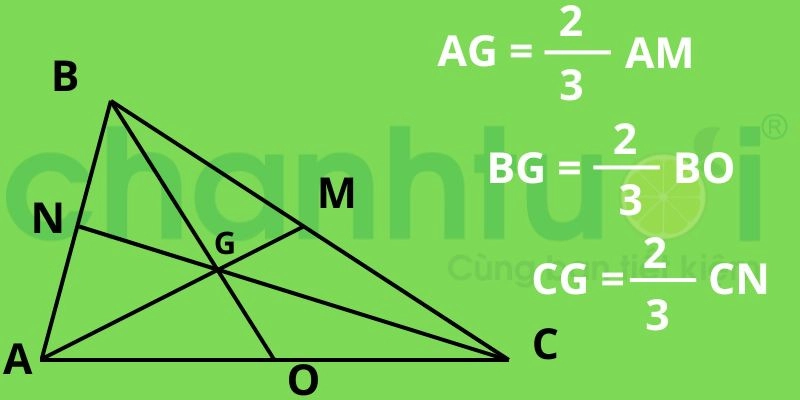 Độ dài đường tâm trong tam giác
Độ dài đường tâm trong tam giác
Công thức tính tọa độ trọng tâm của tam giác là gì?
Công thức tính tọa độ trọng tâm của tam giác áp dụng trong mặt phẳng tọa độ Oxy là phương pháp toán học giúp xác định vị trí trọng tâm của tam giác đó. Để tính tọa độ trọng tâm, ta lấy trung bình tọa độ x, y của 3 đỉnh tam giác.
Cụ thể hơn, để tính tọa độ x của trọng tâm ta lấy trung bình cộng tọa độ x của ba đỉnh tam giác. Đối với tọa độ y của trọng tâm, chúng ta sử dụng giá trị trung bình của tọa độ y tương ứng.
Ví dụ, để tính tọa độ trọng tâm của tam giác ABC có các đỉnh A(x1, y1), B(x2, y2) và C(x3, y3), ta sử dụng công thức sau:
- Tọa độ x trọng tâm = (x1 + x2 + x3) / 3
- Tọa độ trọng tâm y = (y1 + y2 + y3) / 3
Qua ví dụ, với tam giác ABC có các đỉnh A(1, 2), B(4, 6) và C(7, 3), ta có:
- Tọa độ x trọng tâm = (1 + 4 + 7) / 3 = 4
- Tọa độ trọng tâm y = (2 + 6 + 3) / 3 = 3,67 (làm tròn đến hai chữ số thập phân)
Nhờ công thức này, chúng ta có thể dễ dàng tính được tọa độ trọng tâm của bất kỳ tam giác nào trên mặt phẳng tọa độ Oxy.
MUA BỘ QUY TẮC, ĐO BẰNG ĐỘ, SINH VIÊN EKE TẠI ĐÂY
Bài tập về trọng tâm của tam giác
Bài tập 1
Tam giác ABC có đường trung tuyến AD = 9cm và trọng tâm I. Tính độ dài đoạn thẳng AI?
Hướng dẫn giải pháp:
Ta có I là trọng tâm của tam giác ABC và AD là đường trung tuyến nên AI = (2/3) AD (theo 3 đường trung tuyến của tam giác).
Do đó: AG = (2/3).9 = 6 (cm).
Vậy đoạn AI có độ dài 6 cm.
Bài tập 2
Cho tam giác vuông ABC tại A có G là trọng tâm. Chứng minh tam giác AIB và tam giác AIC là tam giác cân.
Hướng dẫn giải pháp:
Cho tam giác ABC vuông tại A, lấy G là trọng tâm. Vì AI là đường trung bình của góc vuông nên ta có: AI = ½ BC = BI = CI.
Suy ra tam giác AIB và tam giác AIC lần lượt cân tại I.
Bài tập 3
Cho tam giác cân ABC tại A có G là trọng tâm. BG cắt AC tạo thành M, CG cắt AB tại N. Chứng minh:
- Một. BM = CN
- b. BN = AN = CM = AM
Hướng dẫn giải pháp:
Cho tam giác cân ABC tại A có G là trọng tâm.
Theo tính chất đường trung trực của một tam giác cân, AG là đường trung trực, đường trung bình và đường cao của tam giác này.
Suy ra AG vuông góc với BC.
Ngoài ra còn có: AB = AC (vì tam giác cân tại A).
Suy ra BM = CN và BN = AN = CM = AM.
Bài tập 4
Cho tam giác vuông ABC có hai cạnh AB = 3cm, AC = 4cm. Tính khoảng cách từ đỉnh A đến trọng tâm G của tam giác ABC.
Hướng dẫn giải pháp:
Phương pháp giải:
- Áp dụng tính chất ba đường trung tuyến của một tam giác
- Áp dụng nhận xét: Trong một tam giác vuông, đường trung tuyến ứng với cạnh bằng nửa cạnh huyền
Gọi M là trung điểm của BC. Suy ra: AM là đường trung bình ứng với cạnh huyền bằng nửa cạnh huyền nên AM = 1/2BC
BC = √(AB^2 + AC^2) = √( 3^2 + 4^2 ) = 5 cm
=> AM = ½ x 5 = 2,5 cm
Vì G là trọng tâm tam giác ABC nên AG = ⅔ AM = ⅔ * 2,5 = 1,7 cm.
Vậy AG = 1,7 cm.
Bài tập 5
Cho tam giác DEF cân tại D có đường trung tuyến DI.
- Một. Chứng minh tam giác DEI = tam giác DFI.
- b. Góc DIE và góc DIF là gì?
- c. Biết DE = DF = 13cm, EF = 10cm hãy tính độ dài đường trung tuyến DI.
Hướng dẫn giải: ký hiệu: ∆ tam giác; ∠ góc
Một. ∆DEI = ∆DFI có:
DI là cạnh chung; DE = DF (∆DEF nặng); IE = IF (DI là số trung vị) => ∆DEI = ∆DFI
b. Vì ΔDEI = ΔDFI
=> ∠DIE = ∠DIF
Mà ∠BID + ∠DIF = 180 độ (bù nhau)
Vậy ∠DIE = ∠DIF = 90 độ
c. I là trung điểm của EF nên IE = IF = 5cm
∆DEI vuông tại I => DI^2 = DE^2 − EI^2 (định lý Pythagore)
=> DI = √144 = 12cm.
Một số câu hỏi liên quan
1. Tiêu điểm nằm ở giao điểm của ba đường thẳng nào?
Trọng tâm của tam giác được xác định bằng giao điểm của ba đường trung tuyến của tam giác đi qua các đỉnh của tam giác và trung điểm tương ứng của các cạnh.
2. Trực tâm của một tam giác là gì?
Trực tâm của một tam giác là giao điểm của ba đường cao trong tam giác đó. Hay thường gọi là tâm tam giác (tam giác đồng quy).
Có thể bạn sẽ quan tâm đến một số công thức khác liên quan đến tam giác:
- Tổng hợp công thức tính chu vi hình tam giác chính xác nhất
- Công thức tính diện tích hình tam giác chính xác nhất
Như vậy, Chánh Tươi Review vừa chia sẻ đến các bạn thông tin về tâm của tam giác, cách xác định và những tính chất nổi bật của nó. Chúc các bạn thành công trong các bài toán liên quan đến trọng tâm là gì và trọng tâm của tam giác là gì!