Trực tâm là gì? Xác định trực tâm trong tam giác

Trong hình học, trực tâm là một khái niệm quan trọng đối với các tam giác nhọn, tù và vuông. Đây là điểm đặc biệt nằm trong tam giác, liên quan chặt chẽ với ba độ cao. Loại đường này còn có nhiều đặc tính độc đáo và có ứng dụng trong nhiều lĩnh vực khác nhau. Bài viết này sẽ giới thiệu chi tiết tất cả các thông tin liên quan đến trực tâm là gì. Đồng thời, bài viết sẽ đưa ra một số bài tập ví dụ để giúp người đọc hiểu rõ hơn về cách vận dụng kiến ​​thức này vào thực tế.

Chánh niệm là gì?

Trực tâm còn thường được gọi là giao điểm độ cao. Vậy chánh niệm là gì? Một tam giác có một góc vuông và các đỉnh của tam giác nằm trên trực tâm của nó. Giao điểm của đường cao này là đoạn thẳng nối trung điểm của cạnh đối diện với góc vuông với tâm của tam giác. Đây cũng là trung điểm của đoạn thẳng nối trọng tâm và đỉnh đối diện với góc vuông.

Để xác định trực tâm của một tam giác, chúng ta chỉ cần vẽ ba đường trung tuyến và tìm giao điểm của chúng. Nó cũng có thể được xác định theo nhiều cách khác nhau. Phương pháp sử dụng công thức toán học là phổ biến nhất.

Tx = (x1 + x2 + x3)/3 Ty = (y1 + y2 + y3)/3

Trong đó (x1, y1), (x2, y2) và (x3, y3) lần lượt là tọa độ của ba đỉnh của tam giác và Tx và Ty lần lượt là tọa độ của trực tâm.

Vai trò của chánh niệm

Trực tâm là một điểm quan trọng trong hình học và có nhiều ứng dụng trong lĩnh vực này. Một trong những ứng dụng quan trọng nhất của trực tâm là tính diện tích hình tam giác. Diện tích của một hình tam giác bằng một nửa tích của chiều dài đáy và chiều cao tương ứng với đáy đó. Giao điểm của đường cao là tâm của đường tròn nội tiếp tam giác, chiều cao tương ứng với đáy là khoảng cách từ trực tâm đến đáy. Do đó, chúng ta có thể tính diện tích của tam giác như sau:

S = 1/2 x AB x HC

Trong đó AB là độ dài đáy của tam giác và HC là khoảng cách từ trực tâm đến đáy AB.

Ngoài ra, giao điểm đường cao còn đóng vai trò quan trọng trong việc xác định các đường trung trực, phân giác vuông góc của tam giác. Đường trung trực của một cạnh là đường thẳng đi qua trực tâm và vuông góc với cạnh đó. Đường trung tuyến của một cạnh là đường thẳng đi qua tâm vuông góc và nối điểm cuối của cạnh đó với đỉnh tương ứng với cạnh đó.

tính chất trực tiếp

Trực tâm của một tam giác là giao điểm của đường trung trực và đường phân giác của tam giác. Nó cũng có thể được định nghĩa là điểm mà ba đường phân giác vuông góc cắt nhau.

Một tính chất thú vị khác của trực tâm là nó cách các đỉnh của tam giác một khoảng bằng nhau. Điều này có nghĩa là nếu chúng ta đo độ dài từ giao điểm của đường cao đến từng đỉnh của tam giác. Sau đó họ sẽ bằng nhau.

Đường thẳng này cũng là tâm của đường tròn ngoại tiếp tam giác, là đường tròn lớn nhất có thể vẽ được qua ba đỉnh của tam giác.

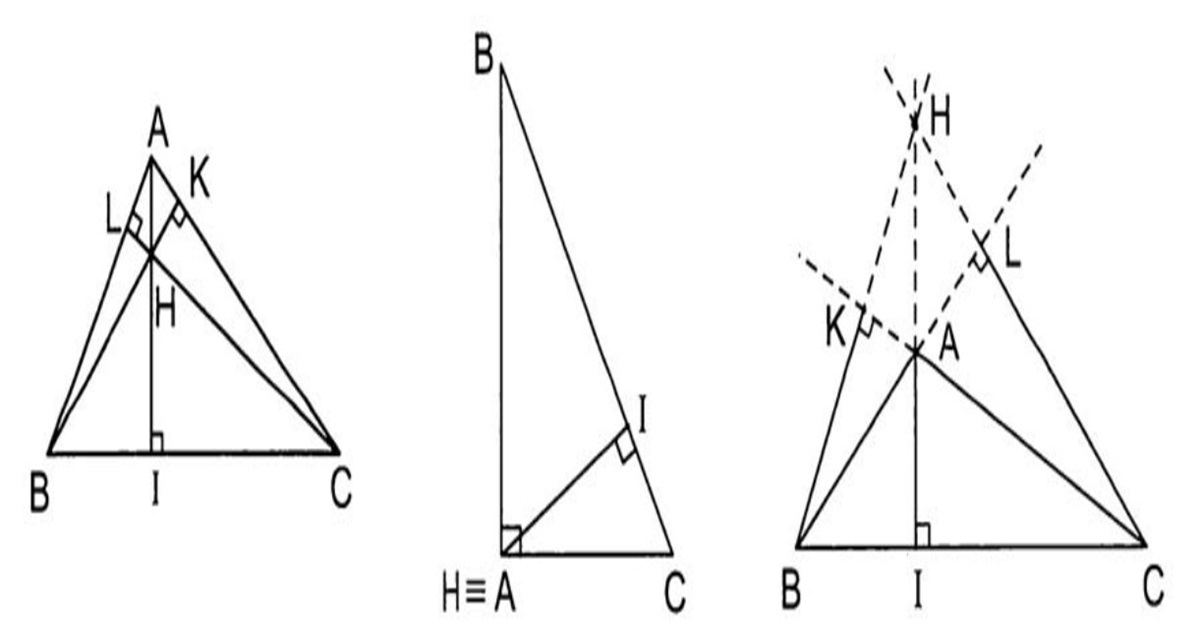
Giao điểm đường cao của tam giác nhọn nằm bên trong tam giác đó. Trong khi đó, giao điểm đường cao của tam giác tù lại nằm ngoài tam giác đó. Điều này phản ánh sự khác biệt về vị trí trực tâm của các loại tam giác khác nhau.

Nếu là tam giác vuông thì trực tâm sẽ nằm trên cạnh huyền và nằm giữa hai đỉnh vuông góc của tam giác.

Nếu chúng ta vẽ các đường thẳng từ các đỉnh của tam giác đến trực tâm thì chúng sẽ cắt các cạnh của tam giác thành các đoạn thẳng vuông góc với các cạnh đó.

Giao điểm độ cao cũng có thể được sử dụng để xác định độ dài các cạnh của một tam giác. Nếu ta biết độ dài các đoạn thẳng từ trực tâm đến các đỉnh của tam giác. Chúng ta có thể tính độ dài các cạnh của một tam giác bằng định lý Pythagoras hoặc các công thức hình học khác.

Cách xác định tâm trực tiếp

Chánh niệm là gì? Làm thế nào để xác định? Xin vui lòng đọc toàn bộ phần này.

Đối với các tam giác nhọn, cân, đều

Để xác định giao điểm của đường cao này, chúng ta có thể vẽ hai đường cao từ hai đỉnh của tam giác và nơi chúng giao nhau là trực tâm. Hoặc chúng ta có thể vẽ đường trung tuyến từ một đỉnh đến trung điểm của cạnh đối diện. Và vẽ một đường vuông góc từ đỉnh đó xuống đường trung tuyến. Nơi hai đường này giao nhau là trực tâm.

Đối với hình tam giác tù

Trực tâm nằm bên ngoài tam giác và gần trung điểm của các đoạn thẳng nối các đỉnh. Để xác định trực tâm của một tam giác tù, ta cũng vẽ hai đường cao của hai đỉnh của tam giác. Nhưng chúng ta cần vẽ một đường cao từ đỉnh góc tù xuống phía đối diện. Giao điểm độ cao là nơi độ cao mới giao với độ cao khác. Nó nằm bên ngoài tam giác đó và ở gần trung điểm của các đoạn thẳng nối các đỉnh.

Đối với tam giác vuông

Trực tâm của tam giác vuông trùng với đỉnh của góc vuông. Điều này xuất phát từ việc hai cạnh tạo thành một góc vuông cũng chính là đường cao của tam giác. Do đó, không cần phải vẽ thêm đường cao hay tìm giao điểm khác, tâm này chính là đỉnh của góc vuông.

Trực tâm là một điểm rất quan trọng vì nó là tâm đường tròn ngoại tiếp tam giác. Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác và có trực tâm là tâm. Nó cũng là tâm của đường tròn tương ứng với tam giác đối diện.

Việc xác định giao điểm độ cao cũng có thể được sử dụng để giải các bài toán liên quan đến hình tam giác. Ví dụ, tìm tâm của hình tròn nội tiếp, tâm của hình tròn ngoại tiếp, tâm của hình tròn đối diện, tâm của nửa hình tròn nội tiếp và nửa hình tròn ngoại tiếp.

Ứng dụng thực tế của trực tâm

Sau khi hiểu được thế nào là trực tâm. Chúng ta sẽ đi vào ứng dụng thực tế của trực tâm để xem nó hữu ích như thế nào.

Kiến trúc và xây dựng

Việc bố trí các cột trụ tại vị trí được xác định qua trực tâm giúp tăng khả năng chịu lực của công trình. Trọng lực từ các phần trên cao của tòa nhà được truyền xuống đáng kể qua các trụ đỡ. Và việc đặt chúng ở những vị trí chiến lược giúp giảm nguy cơ sụp đổ.

Quy hoạch đô thị

Orthocenter có thể được sử dụng để xác định trung tâm của một cộng đồng hoặc khu vực thành phố và từ đó, các nhà quy hoạch có thể đưa ra quyết định về nơi lắp đặt các trạm dịch vụ như bệnh viện, trường học, công viên hoặc các cơ sở công cộng khác. Việc tập trung các dịch vụ này xung quanh một trung tâm có thể giúp tối ưu hóa tiện ích và sự thuận tiện cho người dân địa phương.

Quy hoạch đô thị tích hợp nút giao thông này có thể góp phần xây dựng thành phố thông minh. Dữ liệu vị trí được thu thập từ trung tâm có thể được kết hợp với công nghệ thông tin để cải thiện quản lý giao thông, dịch vụ công cộng và an ninh, tạo ra môi trường sống hiệu quả và thoải mái.

Nghiên cứu đất đai

Trong lĩnh vực nghiên cứu đất, việc xác định trực tâm có thể được thực hiện thông qua các phương pháp đo chính xác. Giống như tất cả GPS (Hệ thống định vị toàn cầu), thiết bị định vị vệ tinh,… Hoặc các kỹ thuật đo địa lý chính xác khác. Sau khi được xác định, các trạm đo đất sẽ được đặt xung quanh điểm để đảm bảo dữ liệu thu thập được mang tính đại diện cho toàn bộ khu vực quan tâm.

Hệ thống điều khiển robot

Thường được tích hợp với các hệ thống đo lường, chẳng hạn như cảm biến vị trí, hệ thống GPS hoặc các thiết bị đo vị trí vệ tinh khác. Điều này giúp xác định chính xác vị trí tuyệt đối của robot trong không gian toàn cầu. Các đoạn đường nối tâm này với các đỉnh của tam giác cung cấp cơ sở hình học vững chắc để xác định vị trí tương đối của robot trong một môi trường cụ thể.

giáo dục hình học

Giao lộ độ cao là một ví dụ giáo dục thực tế trong dạy học hình học. Giúp học sinh hiểu rõ hơn về đặc điểm, tính chất. Từ đó phát triển kỹ năng giải quyết vấn đề và tư duy hình học.

Ứng dụng trong công nghiệp và công nghệ

Trong môi trường công nghiệp, giám sát quy trình từ xa rất quan trọng để đảm bảo an toàn và hiệu suất. Sử dụng orthocenters giúp xác định vị trí của thiết bị và nhân sự. Đồng thời, nó cung cấp dữ liệu chính xác cho hệ thống giám sát từ xa. Điều này có thể được áp dụng trong các nhà máy sản xuất, khu vực nhà kho và các môi trường công nghiệp khác.

Một số bài tập có giải thích dễ hiểu về trực tâm

Bài 1: Cho tam giác vuông ABC có trực tâm H. Biết AB = 3, AC = 4 và BC = 5. Tính độ dài đoạn thẳng AH.

Phần thưởng:

Ta có: AH = 2.HN (với N là trung điểm BC)

Vì tam giác ABC có trực tâm H nên ta có:

BN = CN = một

AH = 2.HN = 2.(BC/2 – a) = BC – 2a

Áp dụng định lý Pytago trong tam giác vuông ABC:

BC^2 = AB^2 + AC^2

5^2 = 3^2 + 4^2

25 = 9 + 16

a^2 = 25/4

a = 5/2

Vì thế:

AH = BC – 2a = 5 – 2,5/2 = 5/2

Bài 2: Cho tam giác ABC có trực tâm H. Biết AB = 8, AC = 10 và BC = 12. Tính diện tích tam giác ABC.

Phần thưởng:

Vì tam giác ABC có trực tâm H nên ta có:

HN = (BN + CN)/2 = BC/2

Áp dụng công thức tính diện tích tam giác:

S = 1/2 . AB . AC . tội lỗi(A)

Gọi A là góc giữa AB và AC.

Chúng ta có thể tính sin(A) bằng cách áp dụng định lý cosin trong tam giác ABC:

BC^2 = AB^2 + AC^2 – 2AB.AC.cos(A)

12^2 = 8^2 + 10^2 – 2.8.10.cos(A)

144 = 164 – 160cos(A)

cos(A) = 5/8

sin(A) = √(1 – cos^2(A)) = √(1 – 25/64) = √(39/64)

Vì thế:

S = 1/2 . AB . AC . sin(A) = 1/2 . 8 . 10 . √(39/64) = 20√39/4

Bài 3: Cho tam giác ABC có trực tâm H. Biết AB = 7, AC = 9 và AH = 4. Tính độ dài đoạn BH.

Phần thưởng:

Vì tam giác ABC có trực tâm H nên ta có:

AH = 2.HN (với N là trung điểm BC)

Vì thế:

HN = AH/2 = 2

Áp dụng định lý Pytago trong tam giác vuông ABH:

BH^2 = AH^2 + AB^2/4

BH^2 = 4^2 + 7^2/4

BH^2 = 16 + 49/4

BH = √(16 + 49/4) = √(113)/2

Kết luận

Trực tâm là giao điểm của ba đường cao. Nó liên quan chặt chẽ đến cấu trúc hình tam giác và có nhiều tính chất đặc biệt. Bài viết trên đã trình bày chi tiết về trực tâm. Thông qua bài viết Tâm trực tiếp là gì? Người đọc có thể hiểu được khái niệm cũng như cách xác định, tính toán tọa độ thông qua các công thức toán học.

Ngoài ra, nó còn có ứng dụng trong kiến ​​trúc, quy hoạch đô thị, nghiên cứu đất đai, hệ thống điều khiển robot, v.v. Hay thậm chí là giáo dục hình học và các ứng dụng công nghiệp khác. Thông qua tìm hiểu về trực tâm, người đọc có thể nắm bắt được tầm quan trọng của nó trong lĩnh vực hình học và ứng dụng thực tế.

Đừng quên theo dõi Thác Trầm Hương Mobile để không bỏ lỡ bất kỳ tin tức nóng hổi nào nhé. Mọi thông báo về sản phẩm mới, khuyến mãi hấp dẫn, độc đáo chỉ có tại Thác Trầm Hương Mobile.

Xem thêm:

• Tính chất của trọng tâm và cách xác định trọng tâm của tam giác trong Hình học
• Đường trung tuyến là gì? Tính chất, công thức và bài tập tính đường trung tuyến